题目内容
已知集合M={2，log2a}，N={a，b}，若M∩N={0}，则M∪N=（ ）
| A、{0，1} |
| B、{0，1，2} |
| C、{1，2} |
| D、{0，2} |
考点：交集及其运算
专题：集合
分析：由已知得log2a=0，解得a=1，从而b=0，由此能求出M∪N．
解答：
解：∵集合M={2，log2a}，N={a，b}，M∩N={0}，
∴log2a=0，解得a=1，
∴b=0，
∴M∪N={0，1，2}．
故选：B．
∴log2a=0，解得a=1，
∴b=0，
∴M∪N={0，1，2}．
故选：B．
点评：本题考查集合的并集的求法，是基础题，解题时要认真审题．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
sin165°•cos75°+cos15°•sin75°=（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
| D、1 |
用演绎法证明函数y=x3是增函数时的大前提是（ ）
| A、增函数的定义 |
| B、函数y=x3满足增函数的定义 |
| C、若x1＜x2，则f（x1）＜f（x2） |
| D、若x1＞x2，则f（x1）＞f（x2） |
在函数y=tanx、y=|sinx|、y=cos（2x+
）中，最小正周期为π的函数的个数为（ ）
| 2π |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
若
=
=
，则△ABC是（ ）
| sinA |
| a |
| cosB |
| b |
| cosC |
| c |
| A、等腰直角三角形 |
| B、有一个内角是30°的直角三角形 |
| C、等边三角形 |
| D、有一个内角是30°的等腰三角形 |
曲线y=x3+1在x=1处的切线方程是（ ）
| A、x=1 |
| B、y=3x-1 |
| C、y=2x-2 |
| D、y=4x-2 |
已知一圆锥的侧面展开图是一个中心角为直角的扇形，若该圆锥的侧面积为4π，则该圆锥的体积为（ ）
A、
| ||||
B、
| ||||
| C、3π | ||||
D、
|
有不同的语文书9本，不同的数学书7本，不同的英语书5本，从中选出不属于同一学科的书2本，则不同的选法有（ ）种．
| A、21 | B、315 |
| C、143 | D、153 |
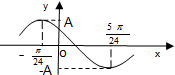已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-