题目内容
已知S、A、B、C是球O表面上的四个点,SA⊥平面ABC,AB⊥BC,SA=2,AB=BC=
,则球O的表面积为 .
| 2 |
考点:球的体积和表面积
专题:空间位置关系与距离
分析:根据题意,三棱锥S-ABC扩展为长方体,长方体的外接球的球心就是长方体体对角线的中点,求出长方体的对角线的长度,即可求解球的半径,从而可求三棱锥S-ABC的外接球的表面积.
解答:
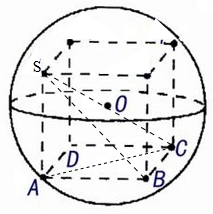 解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=2,AB=BC=
解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=2,AB=BC=
,
三棱锥扩展为长方体的外接球,外接球的直径就是长方体的对角线的长度,
∴球的半径R=
=
=
.
球的表面积为:4πR2=4π•(
)2=8π.
故答案为:8π.
 解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=2,AB=BC=
解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=2,AB=BC=| 2 |
三棱锥扩展为长方体的外接球,外接球的直径就是长方体的对角线的长度,
∴球的半径R=
| 1 |
| 2 |
22+
|
| 2 |
球的表面积为:4πR2=4π•(
| 2 |
故答案为:8π.
点评:本题考查三棱锥S-ABC的外接球的表面积,解题的关键是确定三棱锥S-ABC的外接球的球心与半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
双曲线
-
=1的渐近线方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
过椭圆
+
=1(a>b>0)的两个焦点作垂直x轴的直线与椭圆有四个交点,这四个交点恰好为正方形的四个顶点,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
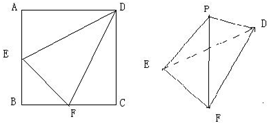 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC