题目内容
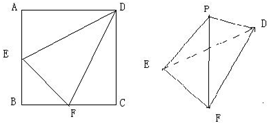 边长为2的正方形ABCD中,E∈AB,F∈BC
边长为2的正方形ABCD中,E∈AB,F∈BC(1)如果E、F分别为AB、BC中点,分别将△AED、△DCF、△BEF沿ED、DF、FE折起,使A、B、C重合于点P.证明:在折叠过程中,A点始终在某个圆上,并指出圆心和半径.
(2)如果F为BC的中点,E是线段AB上的动点,沿DE、DF将△AED、△DCF折起,使A、C重合于点P,求三棱锥P-DEF体积的最大值.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)根据三角形在折叠过程的点的变化,即可得到结论.
(2)根据线面垂直的性质,结合三棱锥的体积公式即可得到结论.
(2)根据线面垂直的性质,结合三棱锥的体积公式即可得到结论.
解答:
解:(1)∵E、F分别为AB、BC中点,在平面图形中连结AF,BD交O点,AF交DE于M,则O为三角形DEF的垂心,
三角形AED在沿DE的折叠过程中,AM始终垂直于DE,
∴过A在过M且与DE垂直的平面上,
又AM=
,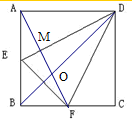
∴A在以M为圆心,AM为半径的圆上.
(2)由于PD⊥PF,PD⊥PE,
故PD⊥平面PEF,
∴当三角形PEF面积最大时,三棱锥P-DEF体积最大,
设PE=t,∠EPF=α,则(2-t)2+1=1+t2-2tcosα,
即cosα=
,
则S△PEF=
t•
=
•
,
故当t=
时,体积最大为
.
三角形AED在沿DE的折叠过程中,AM始终垂直于DE,
∴过A在过M且与DE垂直的平面上,
又AM=
| 2 | ||
|

∴A在以M为圆心,AM为半径的圆上.
(2)由于PD⊥PF,PD⊥PE,
故PD⊥平面PEF,
∴当三角形PEF面积最大时,三棱锥P-DEF体积最大,
设PE=t,∠EPF=α,则(2-t)2+1=1+t2-2tcosα,
即cosα=
| 2t-2 |
| t |
则S△PEF=
| 1 |
| 2 |
1-(
|
| 1 |
| 2 |
| -3t2+8t-4 |
故当t=
| 4 |
| 3 |
2
| ||
| 9 |
点评:本题主要考查考查空间几何体的折叠问题,以及三棱锥的体积计算,综合性较强,难度较大.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知直线l1:y=k1x+b1与l2:y=k2x+b2,则k1=k2是l1∥l2的( )
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要条件 |
复数6i7+8i2014(其中i是虚数单位)在复平面上对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
△ABC的内角A,B,C的对边a,b,c成等差数列,且5sinA=7sinB,则角A=( )
A、
| ||
B、
| ||
C、
| ||
D、
|