题目内容
已知函数f（x）=
的定义域是R，则实数m的取值范围是 ．
| 1 | ||
lg(5x+
|
考点：函数恒成立问题,函数的定义域及其求法
专题：函数的性质及应用
分析：要使定义域为R，即分母不为零恒成立，真数大于零且不等于1恒成立，由此求解；要注意基本不等式的适用条件．
解答：
解：
由题意要使原式恒有意义，只需5x+
+m＞0且≠1恒成立，
即m＞-(5x+
)且m≠1-(5x+
)恒成立，所以m＞-(5x+
)max且y=m与y=1-(5x+
)的图象无交点，
因为5x+
≥2
=4，所以-(5x+
)≤-4，
所以m＞-4且m＞-3，故m＞-3为所求．
故答案为m＞-3．
由题意要使原式恒有意义，只需5x+
| 4 |
| 5x |
即m＞-(5x+
| 4 |
| 5x |
| 4 |
| 5x |
| 4 |
| 5x |
| 4 |
| 5x |
因为5x+
| 4 |
| 5x |
5x×
|
| 4 |
| 5x |
所以m＞-4且m＞-3，故m＞-3为所求．
故答案为m＞-3．
点评：本题容易出错，要注意分母真数不为1恒成立咋考虑，借助于函数图象容易理解，请同学们注意体会．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图，矩形ABCD，点A，B分别在x正半轴和y正半轴上，点C，D在第一象限内|
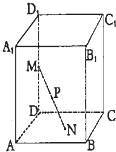已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3，∠BAD=60°长为2的线段MN的一个端点M在DD1上运动，另一个端点N在底面ABCD上运动，则MN的中点P的轨迹（曲面）与共一顶点D的三个面所围成的几何体的体积为（ ）