题目内容
求y=(sinx+
)(cosx+
),x∈[0,
]的最大值.
| 2 |
| 2 |
| π |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:利用三角恒等变换可得y=sinxcosx+
(sinx+cosx)+2,令t=sinx+cosx,易求t∈[1,
],sinxcosx=
,于是有y=
t2+
t+
,利用二次函数的性质可求得x∈[0,
]的最大值.
| 2 |
| 2 |
| t2-1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| π |
| 2 |
解答:
解:y=sinxcosx+
(sinx+cosx)+2(2分)
令t=sinx+cosx=
sin(x+
)(4分)
∵0≤x≤
,∴
≤x+
≤
,∴sin(x+
)∈[
,1],
∴t∈[1,
](6分)
t2=1+2sinxcosx,∴sinxcosx=
,
∴y=
t2+
t+
,
对称轴:t=
=-
∉[1,
](8分)
∴ymax=y(
)=1+2+
=
(10分)
| 2 |
令t=sinx+cosx=
| 2 |
| π |
| 4 |
∵0≤x≤
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴t∈[1,
| 2 |
t2=1+2sinxcosx,∴sinxcosx=
| t2-1 |
| 2 |
∴y=
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
对称轴:t=
| ||
-2×
|
| 2 |
| 2 |
∴ymax=y(
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
点评:本题考查三角函数的最值,着重考查三角恒等变换,突出考查换元法的应用及二次函数的性质,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
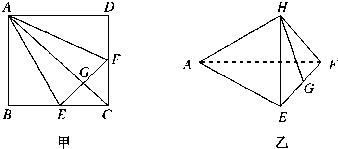
如图甲所示,在正方形ABCD中,EF分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A-EFH中必有( )

| A、AH⊥△EFH所在平面 |
| B、AG⊥△EFH所在平面 |
| C、HF⊥△AEF所在平面 |
| D、HG⊥△AEF所在平面 |
不等式|4-x2|+
≥0的解集是( )
| |x| |
| x |
A、{x|x≤-
| ||||
| B、{x|x>0} | ||||
C、{x|x≤-
| ||||
D、{x|x≤-
|
 如图是各棱长均相等的正四棱锥表面展开图,T为QS的中点,则在四棱锥中PQ与RT所成角的余弦值为
如图是各棱长均相等的正四棱锥表面展开图,T为QS的中点,则在四棱锥中PQ与RT所成角的余弦值为