题目内容
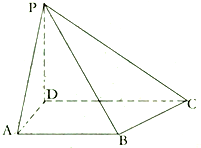 如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=
如图,四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,∠ADC=90°,且CD=2,AD=| 2 |
| PE |
| PC |
(1)当λ=
| 1 |
| 3 |
(2)是否存在λ,使面EBD与面PBC所成二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
考点:用空间向量求平面间的夹角,直线与平面平行的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)首先利用边的关系求出,AC和BD的长,进一步利用△AOB∽△COD,得出
=
=
,最后得出直线PA∥平面EBD
(2)建立空间直角坐标系:先假设存在实数λ,使面EBD与面PBC所成二面角为直二面角,则:根据PD⊥平面∴P(0,0,1),B(
,1,0),C(0,2,0),设面PBC的法向量为:
=(x,y,z)
则:
=(
,1,-1),
=(0,2,-1),
,解得:
=(
,1,2),利用
=λ
.进一步求得:E(2λ,0,1-λ)
=(2λ-
,-1,1-λ),
=(2λ,0,1-λ),进一步设:面EBD的法向量为:
=(m,n,p),
,解得
=(1,
,
),所以利用
•
=0,解得:λ=
,得出存在实数.
| PE |
| EC |
| ( ) |
| ( ) |
| AO |
| CO |
| 1 |
| 2 |
(2)建立空间直角坐标系:先假设存在实数λ,使面EBD与面PBC所成二面角为直二面角,则:根据PD⊥平面∴P(0,0,1),B(
| 2 |
| n1 |
则:
| PB |
| 2 |
| PC |
|
| n1 |
| ||
| 2 |
| PE |
| PC |
| EB |
| 2 |
| DE |
| n2 |
|
| n2 |
| 2 |
| 2λ |
| λ-1 |
| n1 |
| n2 |
12
| ||
| 23 |
解答:
(1)证明:连结:AC,BD
在四棱锥P-ABCD中,PD⊥平面ABCD,∠ADC=90°,且CD=2,AD=
,AB=PD=1,
所以:利用勾股定理解得:
AC=
BD=
∵AB∥CD
△AOB∽△COD
=
E在线段PC上移动,且
=
.
∴
=
=
EO∥PA
PA?平面EBD,EO?平面EBD
直线PA∥平面EBD
(2)结论:存在实数λ=
,使面EBD与面PBC所成二面角为直二面角.
解:假设存在λ,使面EBD与面PBC所成二面角为直二面角
建立空间直角坐标系D=xyz
则:根据PD⊥平面ABCD,∠ADC=90°,且CD=2,AD=
,AB=PD=1,
∴P(0,0,1),B(
,1,0),C(0,2,0)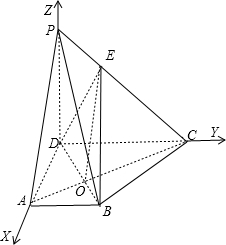
设面PBC的法向量为:
=(x,y,z)
则:
=(
,1,-1),
=(0,2,-1)
解得:
=(
,1,2)
=λ
.
进一步求得:E(2λ,0,1-λ)
=(2λ-
,-1,1-λ),
=(2λ,0,1-λ)
设:面EBD的法向量为:
=(m,n,p)
解得:
=(1,
,
)
所以
•
=0
解得:λ=
故存在实数λ=
,使面EBD与面PBC所成二面角为直二面角.
在四棱锥P-ABCD中,PD⊥平面ABCD,∠ADC=90°,且CD=2,AD=
| 2 |
所以:利用勾股定理解得:
AC=
| 6 |
| 3 |
∵AB∥CD
△AOB∽△COD
| AO |
| CO |
| 1 |
| 2 |
E在线段PC上移动,且
| PE |
| 1 |
| 3 |
| PC |
∴
| PE |
| EC |
| ( ) |
| ( ) |
| AO |
| CO |
| 1 |
| 2 |
EO∥PA
PA?平面EBD,EO?平面EBD
直线PA∥平面EBD
(2)结论:存在实数λ=
12
| ||
| 23 |
解:假设存在λ,使面EBD与面PBC所成二面角为直二面角
建立空间直角坐标系D=xyz
则:根据PD⊥平面ABCD,∠ADC=90°,且CD=2,AD=
| 2 |
∴P(0,0,1),B(
| 2 |

设面PBC的法向量为:
| n1 |
则:
| PB |
| 2 |
| PC |
|
解得:
| n1 |
| ||
| 2 |
| PE |
| PC |
进一步求得:E(2λ,0,1-λ)
| EB |
| 2 |
| DE |
设:面EBD的法向量为:
| n2 |
|
解得:
| n2 |
| 2 |
| 2λ |
| λ-1 |
所以
| n1 |
| n2 |
解得:λ=
12
| ||
| 23 |
故存在实数λ=
12
| ||
| 23 |
点评:本题考查的知识要点:线面平行的判定定理,三角形相似的应用,面面垂直的性质定理,存在性问题的应用,法向量的应用及相关的运算问题.

练习册系列答案
相关题目
集合M={x|(x+2)(x-2)≤0},N={x|-1<x<3},则M∩N=( )
| A、{x|-1≤x<2} |
| B、{x|-1<x≤2} |
| C、{x|-2≤x<3} |
| D、{x|-2<x≤2} |

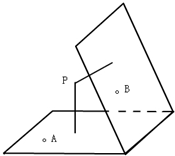 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为