Question

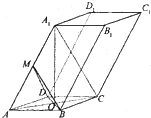已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是边长为2的菱形，AC∩BD=O，AA₁=2

3

，BD⊥A₁A，∠BAD=∠A₁AC=60°，点M是棱AA₁的中点．
（1）求证：A₁C∥平面BMD；
（2）求证：A₁O⊥平面ABCD；
（3）求三棱锥B-AMD的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）根据线面平行的性质即可证明A₁C∥平面BMD；
（2）根据线面垂直的判定定理即可证明A₁O⊥平面ABCD；
（3）利用体积转化法即可求三棱锥B-AMD的体积．

解答： 证明：（1）连结MO，
则

A1M=MA AO=OC

⇒MO∥AC，
∵MO?平面BMD，A₁C?平面BMD，
∴A₁C∥平面BMD．
（2）∵BD⊥AA₁，BD⊥AC，∴BD⊥平面A₁AC，
于是BD⊥A₁O，AC∩BD=O，
∵底面ABCD是边长为2的菱形，且∠BAD=60°，
∴AO=

1

2

AC=

3

，AA₁=2

3

，cos∠A₁AC=60°，
∴A₁O⊥AC，
∵A₁O⊥BD，
∴A₁O⊥平面ABCD；
（3）体积转换法：
∵A₁O⊥平面ABCD，M为A₁O的中点，
∴M到平面ABCD的距离为

1

2

A1O=

3

2

，三角形ABD的面积为

3

，
VB-AMD=VM-ABD=

3

2

．

点评：本题主要考查空间直线和平面平行和垂直的判定以及空间几何体的体积的计算，要求熟练掌握相应的判定定理．