题目内容
设正整数a、b、c（a≤b≤c）和实数x、y、z、ω满足：ax=by=cz=30ω，
+
+
=
，求a、b、c的值．
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| ω |
考点：对数的运算性质,指数式与对数式的互化
专题：函数的性质及应用
分析：首先利用对数解出
，
，
，
，然后代入
+
+
=
，求得abc=30，最后根据abc的大小关系求出只能是a=2，b=3，c=5．
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| ω |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| ω |
解答：
解：设ax=by=cz=30ω=t（t＞0），
因为a、b、c为正整数，所以两边取常用对数得xlga=ylgb=zlgc=wlg30=lgt，
则
=
，
=
，
=
，
=
，
又∵
+
+
=
，
∴
+
+
=
，
∴lga+lgb+lgc=lg30，
∴lg（abc）=lg30，
∴abc=30，
又∵a≤b≤c，
∴a=2，b=3，c=5．
因为a、b、c为正整数，所以两边取常用对数得xlga=ylgb=zlgc=wlg30=lgt，
则
| 1 |
| x |
| lga |
| lgt |
| 1 |
| y |
| lgb |
| lgt |
| 1 |
| z |
| lgc |
| lgt |
| 1 |
| w |
| lg30 |
| lgt |
又∵
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| ω |
∴
| lga |
| lgt |
| lgb |
| lgt |
| lgc |
| lgt |
| lg30 |
| lgt |
∴lga+lgb+lgc=lg30，
∴lg（abc）=lg30，
∴abc=30，
又∵a≤b≤c，
∴a=2，b=3，c=5．
点评：指数与对数的互化以及其运算性质是本题解题的关键，要熟练运用．
练习册系列答案
相关题目
下列说法中，不正确的是（ ）
| A、“|x|=|y|”是“x=y”的必要不充分条件 |
| B、命题p：?x∈R，sinx≤1，则￢p：?x∈R，sinx＞1 |
| C、“λ≤2”是“数列an=n2-λn+1（n∈N*）为递增数列”的充要条件 |
| D、命题p：所有有理数都是实数，q：正数的对数都是负数，则（￢p）∨（￢q）为真命题 |
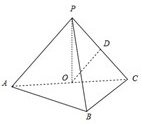如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥平面ABC．