题目内容
(理做)已知函数f(x)=
-lnx,函数y=f(|x|)的零点个数为n,则n=( )
| 1 |
| x-1 |
| A、2 | B、4 | C、6 | D、8 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由于函数f(x)在定义域内不是连续的,所以并不能通过求导递增来直接判断零点的个数,利用数形结合法解决.
解答:
 解:函数f(x)=
解:函数f(x)=
-lnx的定义域为(0,1)∪(1,+∞)
令f(x)=
-lnx=0,可知lnx=
,
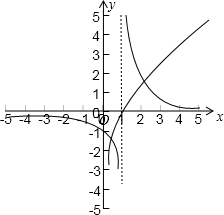
在同一坐标系中,分别画出函数y=lnx与y=
,
由图可知:函数在(0,1)之间有一个零点,在(1,+∞)有一个零点,
又∵函数y=f(|x|)的图象是由函数y=f(x)做一次纵向对折变换得到的,
故函数在(-1,0)之间有一个零点,在(-∞,-1)有一个零点,
函数y=f(|x|)的零点个数为4个,
故选B.
 解:函数f(x)=
解:函数f(x)=| 1 |
| x-1 |
令f(x)=
| 1 |
| x-1 |
| 1 |
| x-1 |
在同一坐标系中,分别画出函数y=lnx与y=
| 1 |
| x-1 |
由图可知:函数在(0,1)之间有一个零点,在(1,+∞)有一个零点,
又∵函数y=f(|x|)的图象是由函数y=f(x)做一次纵向对折变换得到的,
故函数在(-1,0)之间有一个零点,在(-∞,-1)有一个零点,
函数y=f(|x|)的零点个数为4个,
故选B.
点评:本题考查函数的零点,考查数形结合思想的运用,应注意函数f(x)在定义域内不是连续的,所以并不能通过求导递增来直接判断零点的个数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、10 | B、8 | C、3 | D、2 |
设
、
、
是任意的非零平面向量,且相互不共线,则
①(
•
)
=(
•
)
;
②|
|-|
|>|
-
|;
③(
•
)
-(
•
)
与
垂直;
④(3
+2
)•(3
-2
)=9|
|2-4|
|2中,是真命题的有( )
| a |
| b |
| c |
①(
| a |
| b |
| c |
| c |
| a |
| b |
②|
| a |
| b |
| a |
| b |
③(
| b |
| c |
| a |
| c |
| a |
| b |
| c |
④(3
| a |
| b |
| a |
| b |
| a |
| b |
| A、①② | B、②③ | C、③④ | D、②④ |
设A={x||x-a|<1},B={x|(x-1)(5-x)>0},若A∩B=∅,则实数a的取值范围是( )
| A、{a|0≤a≤6} |
| B、{a|a≤2或a≥4} |
| C、{a|a≤0或a≥6} |
| D、{a|2≤a≤4} |
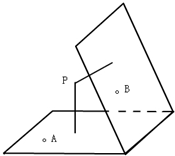 如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为
如图,P为60°的二面角α-l-β内一点,P到二面角两个面的距离分别为2、3,A、B是二面角的两个面内的动点,则△PAB周长的最小值为