Question

对于函数f（x）和g（x），设m∈{x∈R|f（x）=0}，n∈{x∈R|g（x）=0}，若存在m、n，使得|m-n|≤1，则称f（x）与g（x）互为“零点关联函数”．若函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，则实数a的取值范围为（　　）

• A、[2，

  7

  3

  ]
• B、[

  7

  3

  ，3]
• C、[2，3]
• D、[2，4]

Answer 1

考点：函数零点的判定定理

专题：函数的性质及应用

分析：先得出函数f（x）=e^x-1+x-2的零点为x=1．再设g（x）=x²-ax-a+3的零点为β，根据函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，及新定义的零点关联函数，有|1-β|≤1，从而得出g（x）=x²-ax-a+3的零点所在的范围，最后利用数形结合法求解即可．

解答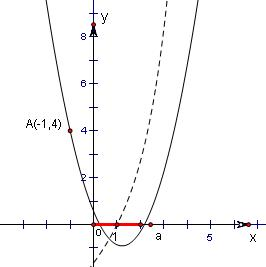： 解：函数f（x）=e^x-1+x-2的零点为x=1．
设g（x）=x²-ax-a+3的零点为β，
若函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，
根据零点关联函数，则|1-β|≤1，
∴0≤β≤2，如图．
由于g（x）=x²-ax-a+3必过点A（-1，4），
故要使其零点在区间[0，2]上，则

g(0)≥0 g( a 2 )≤0

即

-a+3≥0 ( a 2 )2-a× a 2 +3≤0

解得2≤a≤3，
故选：C．

点评：本题主要考查了函数的零点，考查了新定义，主要采用了转化为判断函数的图象的零点的取值范围问题，解题中注意体会数形结合思想与转化思想在解题中的应用