一个几何体的三视图如图所示:则该几何体的外接球表面积为．题目和参考答案——青夏教育精英家教网—

题目内容

一个几何体的三视图如图所示：则该几何体的外接球表面积为

．

考点：棱柱、棱锥、棱台的体积

专题：计算题,空间位置关系与距离

分析：由题意可知三视图复原的几何体是三棱锥，正方体的一个角，根据三视图的数据，求出三棱锥的外接球的表面积即可．

解答： 解：由几何体的三视图知，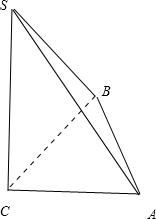

几何体如图所示的三棱锥，
∵几何体的三视图均为腰长为1的等腰直角三角形，
∴SC=AC=BC=2，
且∠SCA=∠SCB=∠ACB=90°，
∵它是棱长为2的正方体的一个角，
∴它的外接球就是棱长为2的正方体的外接球，
外接球的半径R=

，
∴外接球的表面积S=4π（

）²=12π．
故答案为：12π．

点评：本题考查由三视图求几何体的表面积，考查由三视图还原直观图形，考查三棱锥的外接球的表面积，本题是一个基础题．

练习册系列答案

全国名师点拨小学毕业系统总复习系列答案

相关题目

是奇函数．
（Ⅰ）求b的值；
（Ⅱ）判断函数f（x）的单调性；
（Ⅲ）若对任意的t∈R，不等式f（t²-2t）+f（2t²-k）＜0恒成立，求k的取值范围．

已知全集U={1，2，3，4}，集合A={1，2}，B={2，3}，则A∩（∁_UB）等于

．

已知（

+2x）ⁿ展开式中前三项的二项式系数和为37，求n的值．

已知椭圆C的中心在原点，焦点在坐标轴上，短轴的一个端点B（0，4），离心率e=0.6．
（1）求椭圆C的方程；
（2）若O（0，0），P（2，2），试探究在椭圆C内部是否存在整点Q（平面内横、纵坐标都是整数的点为整点），使得△OPQ的面积S_△OPQ=4？若存在，请指出共有几个这样的点（不必具体求出这些点的坐标）；否则，说明理由．

曲线C：（5-m）x²+（m-2）y²=8（m∈R）．
（1）若曲线C表示双曲线，求m的范围；
（2）若曲线C是焦点在x轴上的椭圆，求m的范围；
（3）设m=4，曲线C与y轴交点为A，B（A在B上方），y=kx+4与曲线C交于不同两点M，N，y=1与BM交于G，求证：A，G，N三点共线．

若椭圆

=1的两个焦点F₁，F₂，M是椭圆上一点，且|MF₁|-|MF₂|=1，则△MF₁F₂是（　　）

对于函数f（x）和g（x），设m∈{x∈R|f（x）=0}，n∈{x∈R|g（x）=0}，若存在m、n，使得|m-n|≤1，则称f（x）与g（x）互为“零点关联函数”．若函数f（x）=e^x-1+x-2与g（x）=x²-ax-a+3互为“零点关联函数”，则实数a的取值范围为（　　）