Question

已知正数x、y满足

2x-y≤0 x-3y+5≥0

，则z=3-y(

1

3

)2x的最小值为（　　）

• A、

  1

  9

• B、

  1

  27

• C、

  1

  81

• D、1

Answer 1

考点：有理数指数幂的化简求值

专题：函数的性质及应用,不等式的解法及应用

分析：将z化为3的幂的形式，然后再根据约束条件画出可行域，利用几何意义求最值，只需求出直线z₁=-2x-y过点A（1，2）时，z₁最大值即可．求最小值．

解答： 解：z=3-y(

1

3

)2x=3^-2x-y，设m=-2x-y，要使z最小，则只需求m的最小值即可．
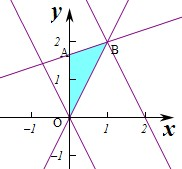
作出不等式组对应的平面区域如图：
由m=-2x-y得y=-2x-m，
平移直线y=-2x-m，由平移可知当直线y=-2x-m，经过点B时，
直线y=-2x-m的截距最大，此时m最小．
由正数x、y满足

2x-y≤0 x-3y+5≥0

，对应的方程组解得B（1，2），此时m=-2-2=-4；
所以z=3^-4=

1

81

；
故选C．

点评：本题主要考查线性规划的应用，利用指数幂的运算性质，整理z为3的幂的形式，只要求出参数m=-2x-y的最小值是解决本题的关键，利用数形结合是解决线性规划题目的常用方