题目内容
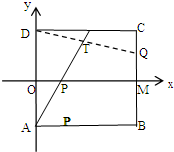 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:交轨法:设M(x,y),由向量关系可得P、Q点的坐标,用λ表示出直线EP、GQ的方程,消掉参数λ即得点M的轨迹方程.
解答:
解:设T(x,y),由已知得P(λ,0),Q(2,1-λ),
则直线TP的方程为y=
-1,直线DQ的方程为y=-
+1,
消去λ即得M的轨迹Γ的方程为
+y2=1(x≠0).
故答案为:
+y2=1(x≠0).
则直线TP的方程为y=
| x |
| λ |
| λx |
| 2 |
消去λ即得M的轨迹Γ的方程为
| x2 |
| 2 |
故答案为:
| x2 |
| 2 |
点评:本题考查交轨法求轨迹方程、椭圆方程等知识,考查方程思想,考查学生解决问题的能力.

练习册系列答案
相关题目
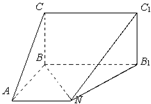 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN=
| 1 |
| 2 |
(1)求证:BN⊥平面C1B1N;
(2)求此五面体的体积.
已知函数y=f(x),下列说法错误的是( )
| A、△y=f(x0+△x)-f(x0)叫函数增量 | ||||
B、
| ||||
| C、f(x)在点x0处的导数记为y′ | ||||
| D、f(x)在点x0处的导数记为f′(x0) |
已知P(3cosα,3sinα,1)和Q(2cosβ,2sinβ,1),则|PQ|的取值范围是( )
| A、[1,5] |
| B、(1,5) |
| C、[0,5] |
| D、[0,25] |