题目内容
已知函数f(x)=sin(2x+
)
(1)求周期,振幅,单调区间,对称轴,对称中心;
(2)指出如何由y=sinx变换得到;
(3)作出一个周期内的图象;
(4)方程f(x)-lgx=0有几个实根?
| π |
| 6 |
(1)求周期,振幅,单调区间,对称轴,对称中心;
(2)指出如何由y=sinx变换得到;
(3)作出一个周期内的图象;
(4)方程f(x)-lgx=0有几个实根?
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象和性质即可求周期,振幅,单调区间,对称轴,对称中心;
(2)根据三角函数图象之间的关系即可得到结论;
(3)作出一个周期内的图象;
(4)将方程f(x)-lgx=0转化为f(x)=lgx,利用数形结合即可得到结论.
(2)根据三角函数图象之间的关系即可得到结论;
(3)作出一个周期内的图象;
(4)将方程f(x)-lgx=0转化为f(x)=lgx,利用数形结合即可得到结论.
解答:
解:(1)∵函数f(x)=sin(2x+
),
∴周期T=
=π,振幅为1,
由2kπ-
≤2x+
≤2kπ+
,
解得kπ-
≤x≤kπ+
,k∈Z,即函数的递增区间为[kπ-
,kπ+
],k∈Z,
由2kπ+
≤2x+
≤2kπ+
,
解得kπ+
≤x≤kπ+
,k∈Z,即函数的递减区间为[kπ+
,kπ+
],k∈Z,
由2x+
=kπ+
,解得x=
+
,即函数的对称轴为x=
+
,
由2x+
=kπ,解得x=
-
,即函数的对称中心为(
-
,0);
(2)将y=sinx的图象沿着x轴向左平移
个单位得到y=sin(x+
),然后纵坐标不变横坐标表位原来的
,即可得到f(x)=sin(2x+
)的图象;
(3)函数在一个周期内的图象;
(4)由f(x)-lgx=0得f(x)=lgx,
作出f(x)和y=lgx的图象可知,两个图象6个交点,
即方程由6个根.
| π |
| 6 |
∴周期T=
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得kπ+
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
由2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
| kπ |
| 2 |
| π |
| 6 |
由2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
| π |
| 12 |
(2)将y=sinx的图象沿着x轴向左平移
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(3)函数在一个周期内的图象;

(4)由f(x)-lgx=0得f(x)=lgx,
作出f(x)和y=lgx的图象可知,两个图象6个交点,
即方程由6个根.

点评:本题主要考查三角函数的图象和性质,要求熟练掌握相应的公式.

练习册系列答案
相关题目
已知圆锥的母线长l=5cm,高h=4cm,则该圆锥的体积是( )cm3.
| A、12π | B、8π |
| C、13π | D、16π |
程序框图是算法思想的重要表现形式,程序框图中不含( )
| A、流程线 | B、判断框 |
| C、循环框 | D、执行框 |
y′=
,则y可以是下列各式中的( )
| 1 |
| x2 |
A、
| ||
B、-
| ||
| C、-2x-3 | ||
D、-
|
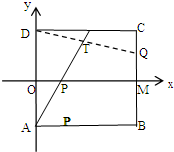 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为