题目内容
设f(x)是定义在R上的增函数,且对于任意的x都有f(1-x)+f(1+x)=0恒成立.如果实数m、n满足不等式组
,那么m2+n2的取值范围是 .
|
考点:抽象函数及其应用
专题:计算题,数形结合,函数的性质及应用,直线与圆
分析:由于对于任意的x都有f(1-x)+f(1+x)=0恒成立,则-f(n2-8n)=f(2-n2+8n),则原不等式组可化为f(m2-6m+23)<f(2-n2+8n),且m>3,再由单调性可得(m-3)2+(n-4)2<4,又m>3,则原不等式组表示的平面区域为右半圆内的部分,由于m2+n2表示点(m,n)与原点的距离d的平方,通过图象观察即可得到取值范围.
解答:
 解:由于对于任意的x都有f(1-x)+f(1+x)=0恒成立,
解:由于对于任意的x都有f(1-x)+f(1+x)=0恒成立,
则-f(n2-8n)=f(2-n2+8n),
即有f(m2-6m+23)+f(n2-8n)<0,
即为f(m2-6m+23)<f(2-n2+8n),
由于f(x)是定义在R上的增函数,
则m2-6m+23<2-n2+8n,
即有(m-3)2+(n-4)2<4,
又m>3,则原不等式组表示的平面区域为右半圆内的部分,
由于m2+n2表示点(m,n)与原点的距离d的平方,
由图象可得d∈(|OA|,|OB|),
即d∈(
,7).
即有m2+n2的取值范围是(13,49).
故答案为:(13,49).
 解:由于对于任意的x都有f(1-x)+f(1+x)=0恒成立,
解:由于对于任意的x都有f(1-x)+f(1+x)=0恒成立,则-f(n2-8n)=f(2-n2+8n),
即有f(m2-6m+23)+f(n2-8n)<0,
即为f(m2-6m+23)<f(2-n2+8n),
由于f(x)是定义在R上的增函数,
则m2-6m+23<2-n2+8n,
即有(m-3)2+(n-4)2<4,
又m>3,则原不等式组表示的平面区域为右半圆内的部分,
由于m2+n2表示点(m,n)与原点的距离d的平方,
由图象可得d∈(|OA|,|OB|),
即d∈(
| 13 |
即有m2+n2的取值范围是(13,49).
故答案为:(13,49).
点评:本题考查抽象函数及运用,考查函数的单调性及应用,考查不等式组表示的平面区域,考查直线与圆的位置关系,以及数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
实数的乘法运算与向量的数量积运算类比,不成立的运算律是( )
A、a×b=b×a类比
| ||||||||||||||
B、a×(b×c)=(a×b)×c类比
| ||||||||||||||
C、a2=|a|2类比
| ||||||||||||||
D、a(b+c)=ab+ac类比
|
函数f(x)=x-lnx的单调递减区间为( )
| A、(-∞,1) |
| B、(1,+∞) |
| C、(0,1) |
| D、(0,+∞) |

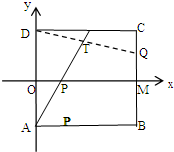 如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为
如图,矩形ABCD中,A(0,-1)D(0,1)B(2,-1)C(2,1),动点P在线段OM上运动,动点Q在线段CB上运动,保持|OP|=|CQ|,则直线AP与DQ的交点T的轨迹方程为