题目内容
函数f（x）=-x2+8x-16在区间[3，5]上（ ）
| A、没有零点 | B、有一个零点 |
| C、有两个零点 | D、无数个零点 |
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：函数f（x）=-x2+8x-16的对称轴为x=4，且f（4）=-16+32-16=0，由二次函数可知有一个零点．
解答：
解：函数f（x）=-x2+8x-16的对称轴为x=4，
且f（4）=-16+32-16=0，
由二次函数的图象可知，
函数f（x）=-x2+8x-16在区间[3，5]上有一个零点．
故选B．
且f（4）=-16+32-16=0，
由二次函数的图象可知，
函数f（x）=-x2+8x-16在区间[3，5]上有一个零点．
故选B．
点评：本题考查了二次函数的性质，同时考查了函数的零点与函数图象的关系，属于基础题．
练习册系列答案
互动课堂系列答案
相关题目
复数
的模是（ ）
| 2-i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设命题p：曲线y=e-x在点（-1，e）处的切线方程：y=-ex；命题q：函数y=sinx+
（0＜x＜π）值域为[4，+∞），则下列判断正确的是（ ）
| 4 |
| sinx |
| A、“p∨q”为真 |
| B、“￢p∨q”为真 |
| C、“￢p∧q”为真 |
| D、“￢p∧￢q”为真 |
若loga（π-3）＜logb（π-3）＜0，a，b为不等于1的正数，则下列不等式中正确（ ）
| A、b＞a＞1 |
| B、a＜b＜1 |
| C、a＞b＞1 |
| D、b＜a＜1 |
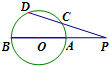如图所示，AB是半径等于3的⊙O的直径，CD是⊙O的弦，BA，DC的延长线交于点P，若PA=4，PC=5，则DC=