题目内容
在△ABC中，已知AB=AC，BC=4，点P在边BC上，
•
的最小值为 ．
| PA |
| PC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：本题可利用等腰三角形底边上的中线垂直于底边，建立平面直角坐标系，设出动点P的坐标，将
•
转化为二次函数在区间上的值域，研究二次函数，得到本题结论．
| PA |
| PC |
解答：
解：∵在△ABC中，已知AB=AC，
∴取BC中点O建立如图所示的平面直角坐标系．
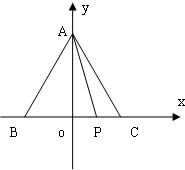
∵BC=4，
∴B（-2，0），C（2，0）．
设A（0，b），P（x，0），（-2≤x≤2）．
∴
=(-x，b)，
=(2-x，0)，
∴
•
=-x（2-x）=x2-2x=（x-1）2-1≥-1．
当且仅当x=1时，取最小值．
∴
•
的最小值为-1．
故答案为：-1．
∴取BC中点O建立如图所示的平面直角坐标系．
∵BC=4，
∴B（-2，0），C（2，0）．
设A（0，b），P（x，0），（-2≤x≤2）．
∴
| PA |
| PC |
∴
| PA |
| PC |
当且仅当x=1时，取最小值．
∴
| PA |
| PC |
故答案为：-1．
点评：本题考查了平面向量的坐标运算，解题时要注意变量x的取值范围，本题思维难度不大，属于基础题，
练习册系列答案
相关题目
已知ω＞0，函数f(x)=sin(ωx+
)在[-
，
]上单调递增．则ω的取值范围是（ ）
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| A、（0，3] | ||
B、(0，
| ||
| C、（0，1] | ||
D、[-
|
已知向量
=（2，x），
=（x，1），若
与
方向相同，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、±4 | ||
B、±
| ||
C、
| ||
D、-
|
下列从集合M到集合N的对应f是映射的是（ ）
A、 |
B、 |
C、 |
D、 |
函数f（x）=-x2+8x-16在区间[3，5]上（ ）
| A、没有零点 | B、有一个零点 |
| C、有两个零点 | D、无数个零点 |