题目内容
设直角三角形的两锐角分别为α,β,则有sinα+sinβ≤
成立,类比到三棱锥中,若三个侧面两侧垂直,三条侧棱与底面所成的角分别为α,β,γ,则有 .
| 2 |
考点:类比推理
专题:推理和证明
分析:由直角三角形的两锐角分别为α,β,则有sinα+sinβ≤
成立,类比推理在空间几何中,若三棱锥的三个侧面两侧垂直,三条侧棱与底面所成的角分别为α,β,γ,则有sinα+sinβ+sinγ≤
.
| 2 |
| 3 |
解答:
解:由直角三角形的两锐角分别为α,β,则有ainα+sinβ≤
,
当ainα=sinβ=
取等号,
类比可得:
若三棱锥的三个侧面两侧垂直,三条侧棱与底面所成的角分别为α,β,γ,则有sinα+sinβ+sinγ≤
.
当且仅当sinα=sinβ=sinγ=
时取等号,
故答案为:sinα+sinβ+sinγ≤
| 2 |
当ainα=sinβ=
| ||
| 2 |
类比可得:
若三棱锥的三个侧面两侧垂直,三条侧棱与底面所成的角分别为α,β,γ,则有sinα+sinβ+sinγ≤
| 3 |
当且仅当sinα=sinβ=sinγ=
| ||
| 3 |
故答案为:sinα+sinβ+sinγ≤
| 3 |
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=-x2+8x-16在区间[3,5]上( )
| A、没有零点 | B、有一个零点 |
| C、有两个零点 | D、无数个零点 |
已知f(x)=10x-1-2,则f(x)的反函数当自变量取98时的函数值是( )
| A、1 | B、2 | C、3 | D、4 |
下列计算不正确的是( )
| A、log3243=log335=5log33=5×1=5 | ||||
B、log510-log52=log5
| ||||
| C、lg2+lg5=lg(2×5)=lg10=1 | ||||
D、log8(8×4)=log88+log84=1+
|
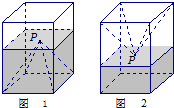 如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:
如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题: