题目内容
 已知向量
已知向量| a |
| b |
| c |
| c |
| a |
| b |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:以
的起点为原点,水平向右的方向为x轴的正方向,建立直角坐标系,可得
、
、
的坐标.再根据
=λ
+μ
求得 λ和μ的值,可得λ+μ的值.
| b |
| a |
| b |
| c |
| c |
| a |
| b |
解答:
解:以
的起点为原点,水平向右的方向为x轴的正方向,建立直角坐标系,
则
=(-1,1),
=(3,3),
=(-1,-3).
再根据 若
=λ
+μ
(λ,μ∈R),可得 (-1,-3)=(3μ-λ,λ+3μ),
∴3μ-λ=-1,λ+3μ=-3,解得 λ=-1,μ=-
,则λ+μ=-
,
故答案为:-
.
| b |
则
| a |
| b |
| c |
再根据 若
| c |
| a |
| b |
∴3μ-λ=-1,λ+3μ=-3,解得 λ=-1,μ=-
| 2 |
| 3 |
| 5 |
| 3 |
故答案为:-
| 5 |
| 3 |
点评:本题主要考查平面向量基本定理、两个向量坐标形式的运算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
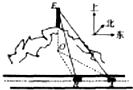 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.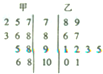 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.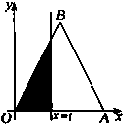 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则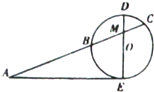 如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=