题目内容
一个几何体的三视图如图所示,则该几何体的体积为 .


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图,可得该几何体是一个以俯视图为底面的三棱锥,求出棱锥的底面面积和高,代入棱锥体积公式,可得答案.
解答:
解:由已知中的三视图,可得该几何体是一个以俯视图为底面的三棱锥,
∵棱锥的底面面积S=
×(4+2)×2=6,
棱锥的高h=2,
故棱锥的体积V=
Sh=4,
故答案为:4
∵棱锥的底面面积S=
| 1 |
| 2 |
棱锥的高h=2,
故棱锥的体积V=
| 1 |
| 3 |
故答案为:4
点评:本题考查的知识点是由三视图求体积,其中分析出几何体的形状是解答的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知弹簧的一端固定在地面上,另一端固定一个小球,已知小球在达到平衡位置之前处于加速状态,且加速度与时间的函数关系为a(t)=2t+
+3,则当t=1时小球的速度为( )
| 10 |
| 1+t |
| A、4+10ln2 |
| B、5+10ln2 |
| C、4-10ln2 |
| D、5-10ln2 |
 已知向量
已知向量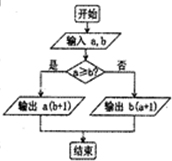 如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan
如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan