题目内容
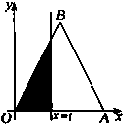 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积为f(t),则(Ⅰ)函数f(t)的解析式为
(Ⅱ)函数y=f(t)的图象在点P(t0,f(t0))处的切线的斜率为
2
| ||
| 3 |
考点:利用导数研究曲线上某点切线方程,函数解析式的求解及常用方法
专题:函数的性质及应用,导数的综合应用
分析:(Ⅰ)结合图形,求出0<t≤1时和1<t≤2时满足条件的图形的面积,用分段函数表示f(t)的解析式;
(Ⅱ)由于函数的图象在点P处的切线的斜率为
,则解关于函数的导数为
方程,即可得到答案.
(Ⅱ)由于函数的图象在点P处的切线的斜率为
2
| ||
| 3 |
2
| ||
| 3 |
解答:
解:(Ⅰ)由图形知,
当0<t≤1时,此时满足条件的图形面积为
f(t)=
•t•t•tan
=
t2;
当1<t≤2时,此时满足条件的图形面积为
f(t)=
×2×1×tan
-
•(2-x)•(2-x)•tan
=
-
(t-2)2;
∴函数f(t)=
;
(Ⅱ)函数y=f(t)的图象在点P(t0,f(t0))处的切线的斜率为
,
则函数在点P(t0,f(t0))处的导数为
,
当0<t≤1时,f(t)=
t2,则f′(t)=
t,
即f′(t0)=
t0=
,解得t0=
;
当1<t≤2时,f(t)=
-
(t-2)2,则f′(t)=-
(t-2),
即f′(t0)=-
(t0-2)=
,解得t0=
,
故t0=
或
.
故答案为:(Ⅰ)f(t)=
;(Ⅱ)
或
.
当0<t≤1时,此时满足条件的图形面积为
f(t)=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
当1<t≤2时,此时满足条件的图形面积为
f(t)=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 3 |
| ||
| 2 |
∴函数f(t)=
|
(Ⅱ)函数y=f(t)的图象在点P(t0,f(t0))处的切线的斜率为
2
| ||
| 3 |
则函数在点P(t0,f(t0))处的导数为
2
| ||
| 3 |
当0<t≤1时,f(t)=
| ||
| 2 |
| 3 |
即f′(t0)=
| 3 |
2
| ||
| 3 |
| 2 |
| 3 |
当1<t≤2时,f(t)=
| 3 |
| ||
| 2 |
| 3 |
即f′(t0)=-
| 3 |
2
| ||
| 3 |
| 4 |
| 3 |
故t0=
| 2 |
| 3 |
| 4 |
| 3 |
故答案为:(Ⅰ)f(t)=
|
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查了求函数的解析式以及利用导数求切线问题,解题时应结合图形,即可求出符合条件的解析式,是综合题目.

练习册系列答案
相关题目
 已知向量
已知向量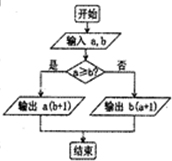 如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan
如图,定义某种运算S=a?b,运算原理如图所示,则式子(2tan