题目内容
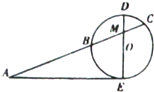如图，AE切圆O于点E，AC交圆O于B，C两点，且与直径DE交于点M，DM=2，CM=3，BM=6，则tanA=考点：与圆有关的比例线段
专题：选作题,立体几何
分析：利用切割线定理、勾股定理，分别表示出AE2，求出AB，可得AE，再利用正切函数，即可得出结论．
解答：
解：设AB=x，则
∵DM=2，CM=3，BM=6，
∴ME=9，
∵DE是直径，AE切圆O于点E，
∴AE2=x•（x+9），
∵AE2=（x+6）2-92，
∴x=15，
∴AE=6
，
∵ME=9，
∴tanA=
=
=
．
故答案为：
．
∵DM=2，CM=3，BM=6，
∴ME=9，
∵DE是直径，AE切圆O于点E，
∴AE2=x•（x+9），
∵AE2=（x+6）2-92，
∴x=15，
∴AE=6
| 10 |
∵ME=9，
∴tanA=
| ME |
| AE |
| 9 | ||
6
|
3
| ||
| 20 |
故答案为：
3
| ||
| 20 |
点评：本题考查切割线定理、勾股定理，考查学生的计算能力，正确表示AE2，是关键．
练习册系列答案
相关题目
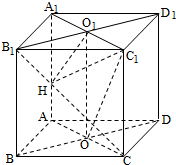如图，四棱柱ABCD-A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．
圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线C1：
已知向量