题目内容
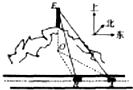如图，一辆汽车在一条水平的公路上向正西方向行驶，在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O（点O是点E在公路所在平面上的射影）的方位角是西偏北φ，再行驶akm到达B处，测得山脚点O的方位角是西偏北β．请设计一个方案，用测量的数据和有关公式写出计算OE的步骤．考点：解三角形的实际应用
专题：应用题,解三角形
分析：第一步，由正弦定理求OA；第二步，OE=OAtanθ，可得结论．
解答：
解：第一步，求OA，在△AOB中，∠ABO=π-β，∠AOB=β-φ，AB=a，
由正弦定理得OA=
=
；
第二步，求OE，在Rt△EOA中，∠EAO=θ，∠EOA=90°，则OE=OAtanθ=
．
由正弦定理得OA=
| asin(π-β) |
| sin(β-φ) |
| asinβ |
| sin(β-φ) |
第二步，求OE，在Rt△EOA中，∠EAO=θ，∠EOA=90°，则OE=OAtanθ=
| asinβtanθ |
| sin(β-φ) |
点评：本题主要考查了解三角形的实际应用．考查了运用数学知识，建立数学模型解决实际问题的能力．
练习册系列答案
相关题目
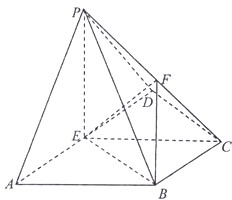如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，ABCD是梯形，BC∥AD，E，F分别是AD，PC的中点，△ABE，△BEC，△ECD都是边长为1的等边三角形．
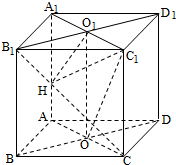如图，四棱柱ABCD-A1B1C1D1的所有棱长都相等，AC∩BD=O，A1C1∩B1D1=O1，四边形ACC1A1和四边形BDD1B1均为矩形．
圆x2+y2=4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为P（如图），双曲线C1：
已知向量