题目内容
已知tanα,tαnβ是方程x2-3x-3=0的两个根,求sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β)的值.
考点:两角和与差的正切函数,三角函数的化简求值
专题:三角函数的求值
分析:利用韦达定理求出tanα+tαnβ,tanαtαnβ,推出tan(α+β),然后化简所求表达式为正切函数的形式,求解即可.
解答:
解:tanα,tαnβ是方程x2-3x-3=0的两个根,
∴tanα+tαnβ=3,tanαtαnβ=-3,
∴tan(α+β)=
=
.
则sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β)
=
=
=
=-3.
∴tanα+tαnβ=3,tanαtαnβ=-3,
∴tan(α+β)=
| tanα+tαnβ |
| 1-tanαtαnβ |
| 3 |
| 4 |
则sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β)
=
| sin2(α+β)-3sin(α+β)cos(α+β)-3cos2(α+β) |
| sin2(α+β)+cos2(α+β) |
=
| tan2(α+β)-3tan(α+β)-3 |
| tan2(α+β)+1 |
=
| ||||
|
=-3.
点评:本题考查两角和与差的三角函数,韦达定理的应用,考查计算能力.

练习册系列答案
相关题目
若sin(x+
)=
,则sin(
π-x)+cos(
-x)值为( )
| π |
| 6 |
| 1 |
| 4 |
| 5 |
| 6 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
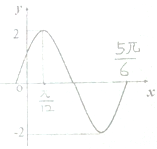 函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(ω>0,|φ|<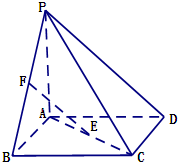 如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.
如图,四棱P-ABCD的底面ABCD为正方形,PA⊥底面ABCD,E、F分别是AC、PB的中点.