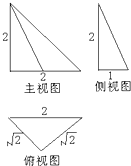
题目内容
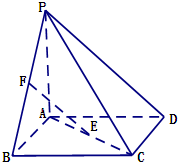如图，四棱P-ABCD的底面ABCD为正方形，PA⊥底面ABCD，E、F分别是AC、PB的中点．（1）求证：EF∥平面PCD；
（2）求证：平面PBD⊥平面PAC．
考点：平面与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）根据线面平行的判定定理即可证明EF∥平面PCD；
（2）根据面面垂直的判定定理即可证明平面PBD⊥平面PAC．
（2）根据面面垂直的判定定理即可证明平面PBD⊥平面PAC．
解答：
解：（1）如图，连结BD，则E是BD的中点，
又F是PB的中点，∴EF∥PD．
又∵EF?平面PCD，PD?面PCD
∴EF∥平面PCD．
（2）∵ABCD是正方形，∴BD⊥AC，
∵PA⊥平面ABC，∴PA⊥BD，
又PA∩AC=A，∴BD⊥面PAC．
又BD?平面PBD，
故平面PBD⊥平面PAC
又F是PB的中点，∴EF∥PD．
又∵EF?平面PCD，PD?面PCD
∴EF∥平面PCD．
（2）∵ABCD是正方形，∴BD⊥AC，
∵PA⊥平面ABC，∴PA⊥BD，
又PA∩AC=A，∴BD⊥面PAC．
又BD?平面PBD，
故平面PBD⊥平面PAC
点评：本题主要考查直线和平行平行以及面面垂直的判定，要求熟练掌握相应的判定定理．
练习册系列答案
相关题目
椭圆的一个顶点为（0，2），离心率为e=
，以坐标轴为对称轴的椭圆方程是（ ）
| 1 |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
