Question

求曲线y=cosx与直线x=

π

2

、x=

3π

2

、y=0所围成的面积．

Answer 1

考点：定积分在求面积中的应用

专题：导数的概念及应用

分析：本题利用直接法求解，根据三角函数的对称性知，曲线y=cosx与直线x=

π

2

、x=

3π

2

、y=0所围成的平面区域的面积S为：曲线y=cosx与直线x=

π

2

，x=π所围成的平面区域的面积的二倍，最后结合定积分计算面积即可．

解答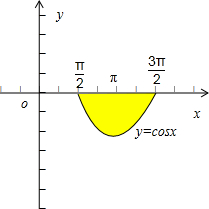： 解：根据对称性，得：
曲线y=cosx与直线x=

π

2

、x=

3π

2

、y=0所围成的平面区域的面积S为：曲线y=cosx与直线x=

π

2

，x=π所围成的平面区域的面积的二倍，∴S=-2

∫

π π 2

cosxdx=-2sinx

|

π π 2

=2．
故曲线y=cosx与直线x=

π

2

、x=

3π

2

、y=0所围成的面积为2．

点评：本小题主要考查定积分应用、三角函数的图象等基础知识，考查考查数形结合思想，属于基础题．