题目内容
已知函数f(x)=lnx-a(1-
),a∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)的最小值为0,回答下列问题:
(ⅰ)求实数a的值;
(ⅱ)设A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)=xf(x)图象上的两点,且曲线g(x)在点T(t,g(t))处的切线与直线AB平行,求证:x1<t<x2.
| 1 |
| x |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)的最小值为0,回答下列问题:
(ⅰ)求实数a的值;
(ⅱ)设A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)=xf(x)图象上的两点,且曲线g(x)在点T(t,g(t))处的切线与直线AB平行,求证:x1<t<x2.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)直接对f(x)求导,讨论a≤0和a>0时,f′(x)的正负即可确定函数f(x)单调区间;
(Ⅱ)(ⅰ)结合(Ⅰ)和f(x)的最小值为0,得到[f(x)]min=f(a)=1-a+lna=0.再由导数研究函数h(x)=1-x+lnx(x>0)的最值,进而求得实数a的值;
(ⅱ)根据导数的几何意义与两点连线的斜率公式,得kAB=g′(t),
令λ=
>1,于是lnt-lnx1=
,得出当λ>1时,lnλ>1-
,于是lnt-lnx1>0,即t>x1成立,
类似的方法可证出当λ>1时,lnλ<λ-1,即-lnλ+λ-1>0,于是lnx2-lnt>0,即x2>t成立.由此即可得到x1<x0<x2成立.
(Ⅱ)(ⅰ)结合(Ⅰ)和f(x)的最小值为0,得到[f(x)]min=f(a)=1-a+lna=0.再由导数研究函数h(x)=1-x+lnx(x>0)的最值,进而求得实数a的值;
(ⅱ)根据导数的几何意义与两点连线的斜率公式,得kAB=g′(t),
令λ=
| x2 |
| x1 |
lnλ-(1-
| ||
1-
|
| 1 |
| λ |
类似的方法可证出当λ>1时,lnλ<λ-1,即-lnλ+λ-1>0,于是lnx2-lnt>0,即x2>t成立.由此即可得到x1<x0<x2成立.
解答:
解:(Ⅰ)函数f(x)的定义域为(0,+∞),且f′(x)=
-
=
.
当a≤0时,f′(x)>0,所以f(x)在区间(0,+∞)单调递增;
当a>0时,由f′(x)>0,解得x>a;由f′(x)<0,解得0<x<a.
所以f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).
综上述:a≤0时,f(x)的单调递增区间是(0,+∞);
a>0时,f(x)的单调递减区间是(0,a),单调递增区间是(a,+∞).
(Ⅱ)(ⅰ)由(Ⅰ)知,当a≤0时,f(x)无最小值,不合题意;
当a>0时,[f(x)]min=f(a)=1-a+lna=0.
令h(x)=1-x+lnx(x>0),则h′(x)=-1+
=
,
由h′(x)>0,解得0<x<1;由h′(x)<0,解得x>1.
所以h(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
故[h(x)]max=h(1)=0,即当且仅当x=1时,h(x)=0.
因此,a=1.
(ⅱ)因为g(x)=xf(x)=xlnx-x+1(x>0),所以g′(x)=lnx
直线AB的斜率kAB=
=
-1,g′(t)=lnt.
依题意,可得kAB=g′(t),即
-1=lnt.
令λ=
>1,
于是lnt-lnx1=
-1-lnx1=
-1
=
-1=
.
由(ⅰ)知,当λ>1时,lnλ>1-
,于是lnt-lnx1>0,即t>x1成立.
lnx2-lnt=lnx2-(
-1)=
+1=
+1
=
=
.
由(ⅰ)知,当λ>1时,lnλ<λ-1,即-lnλ+λ-1>0,于是lnx2-lnt>0,
即x2>t成立.
综上,x1<t<x2成立.
| 1 |
| x |
| a |
| x2 |
| x-a |
| x2 |
当a≤0时,f′(x)>0,所以f(x)在区间(0,+∞)单调递增;
当a>0时,由f′(x)>0,解得x>a;由f′(x)<0,解得0<x<a.
所以f(x)的单调递增区间为(a,+∞),单调递减区间为(0,a).
综上述:a≤0时,f(x)的单调递增区间是(0,+∞);
a>0时,f(x)的单调递减区间是(0,a),单调递增区间是(a,+∞).
(Ⅱ)(ⅰ)由(Ⅰ)知,当a≤0时,f(x)无最小值,不合题意;
当a>0时,[f(x)]min=f(a)=1-a+lna=0.
令h(x)=1-x+lnx(x>0),则h′(x)=-1+
| 1 |
| x |
| 1-x |
| x |
由h′(x)>0,解得0<x<1;由h′(x)<0,解得x>1.
所以h(x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
故[h(x)]max=h(1)=0,即当且仅当x=1时,h(x)=0.
因此,a=1.
(ⅱ)因为g(x)=xf(x)=xlnx-x+1(x>0),所以g′(x)=lnx
直线AB的斜率kAB=
| g(x2)-g(x1) |
| x2-x1 |
| x2lnx2-x1lnx1 |
| x2-x1 |
依题意,可得kAB=g′(t),即
| x2lnx2-x1lnx1 |
| x2-x1 |
令λ=
| x2 |
| x1 |
于是lnt-lnx1=
| x2lnx2-x1lnx1 |
| x2-x1 |
| x2lnx2-x2lnx1 |
| x2-x1 |
=
ln
| ||
1-
|
lnλ-(1-
| ||
1-
|
由(ⅰ)知,当λ>1时,lnλ>1-
| 1 |
| λ |
lnx2-lnt=lnx2-(
| x2lnx2-x1lnx1 |
| x2-x1 |
| x1lnx1-x1lnx2 |
| x2-x1 |
ln
| ||
|
=
ln
| ||
| λ-1 |
| -lnλ+λ-1 |
| λ-1 |
由(ⅰ)知,当λ>1时,lnλ<λ-1,即-lnλ+λ-1>0,于是lnx2-lnt>0,
即x2>t成立.
综上,x1<t<x2成立.
点评:本小题主要考查函数的单调性、函数的最值、导数及其应用等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、数形结合思想等.

练习册系列答案
相关题目
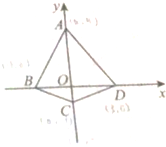 在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.
在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.