题目内容
已知数列{an}满足:an+1=
,a1=2,bn=
(1)求{bn}的通项公式;
(2)求证:当n≥3时,b1+b2+…+bn<
.
| an(an2+3) |
| 3an2+1 |
| an-1 |
| an+1 |
(1)求{bn}的通项公式;
(2)求证:当n≥3时,b1+b2+…+bn<
| 241 |
| 648 |
考点:数列与不等式的综合,数列递推式
专题:计算题,证明题,等差数列与等比数列,二项式定理
分析:(1)求出bn+1,因式分解,得到bn+1=bn3,两边取3为底的对数,得到等比数列,由等比数列的通项公式,即可得到bn;
(2)运用二项式定理,得到当n≥3,3n-1=(1+2)n-1=
+…+
>2n,再由指数函数的单调性,运用等比数列的求和公式,即可得证.
(2)运用二项式定理,得到当n≥3,3n-1=(1+2)n-1=
| C | 0 n-1 |
| +2C | 1 n-1 |
| 2n-1C | n-1 n-1 |
解答:
(1)解:由于an+1=
,bn=
,
则bn+1=
=
=(
)3=bn3,
由于b1=
=
,
则log3bn+1=log3bn3=3log3bn,
即有{log3bn}为等比数列,即有log3bn=log3
•3n-1,
即有bn=(
)3n-1;
(2)证明:当n≥3,3n-1=(1+2)n-1=
+…+
>2n,
则bn=(
)3n-1<(
)2n(n≥3),
故当n≥3时,b1+b2+…+bn<
+
+(
)6+…+(
)2n
=
+
<
+
=
.
即原不等式成立.
| an(an2+3) |
| 3an2+1 |
| an-1 |
| an+1 |
则bn+1=
| an+1-1 |
| an+1+1 |
| an3-3an2+3an-1 |
| an3+3an2+3an+1 |
| an-1 |
| an+1 |
由于b1=
| a1-1 |
| a1+1 |
| 1 |
| 3 |
则log3bn+1=log3bn3=3log3bn,
即有{log3bn}为等比数列,即有log3bn=log3
| 1 |
| 3 |
即有bn=(
| 1 |
| 3 |
(2)证明:当n≥3,3n-1=(1+2)n-1=
| C | 0 n-1 |
| +2C | 1 n-1 |
| 2n-1C | n-1 n-1 |
则bn=(
| 1 |
| 3 |
| 1 |
| 3 |
故当n≥3时,b1+b2+…+bn<
| 1 |
| 3 |
| 1 |
| 27 |
| 1 |
| 3 |
| 1 |
| 3 |
=
| 10 |
| 27 |
| ||||
1-
|
| 10 |
| 27 |
| 1 |
| 648 |
| 241 |
| 648 |
即原不等式成立.
点评:本题考查数列通项公式的求法,考查等比数列的通项和求和公式的运用,考查二项式定理及其运用,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
函数y=
的值域是 ( )
| x2-8x+15 |
| x2-x-6 |
| A、(-∞,1) | ||||
| B、(-∞,1)∪(1,+∞) | ||||
C、(-∞,-
| ||||
D、(-∞,-
|
已知θ∈R时,不等式m2-(1+4sin2θ)m+4-6cos2θ≥0恒成立,则实数m的取值范围是( )
| A、m≥4或m≤1 |
| B、m≥4或m≤-1 |
| C、m≥2或m≤1 |
| D、m≥2或m≤-1 |
 一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为
一流的高尔夫选手约70杆即可打完十八洞,而初学者约160杆才可打完十八洞.如图是甲、乙两位高尔夫选手在五次训练测试中打出的杆数的茎叶图,则发挥比较稳定的选手的方差为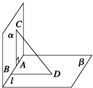 如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )
如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )