题目内容
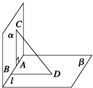如图所示，在直二面角α-l-β中，A，B∈l，AC?α，AC⊥l，BD?β，BD⊥l，|AC|=6，|AB|=8，|BD|=24，则线段CD的长是（ ）| A、25 | B、26 | C、27 | D、28 |
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：直接利用直线的垂直关系，求出向量数量积，然后通过|
|2=|
+
+
|2，求解即可．
| CD |
| CA |
| AB |
| BD |
解答：
解：∵AC⊥AB，BD⊥AB，
∴
•
=0，
•
=0，
•
=0，
=
+
+
，
∴|
|2=|
+
+
|2=
2+
2+
2+2
•
+2
•
+2
•
=676，
∴|
|=26．
故选：B．
∴
| AC |
| AB |
| BD |
| AB |
| AC |
| BD |
| CD |
| CA |
| AB |
| BD |
∴|
| CD |
| CA |
| AB |
| BD |
| CA |
| AB |
| BD |
| AC |
| AB |
| BD |
| AB |
| AC |
| BD |
∴|
| CD |
故选：B．
点评：本题考查空间两点的距离公式的求法，考查计算能力．
练习册系列答案
字词句段篇系列答案
相关题目
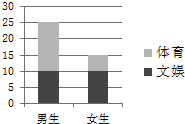对某班学生是更喜欢体育还是更喜欢文娱进行调查，根据调查得到的数据，所绘制的二维条形图如图．
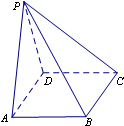如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA=PD=