题目内容
已知|
|=|
|=2,若函数f(x)=|
+x
|(x∈R)的最小值为1,则
•
= .
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算,绝对值不等式的解法
专题:函数的性质及应用,平面向量及应用
分析:由|
|=|
|=2,函数f(x)=|
+x
|(x∈R)的最小值为1,可得
2x2+2
•
x+
2 的最小值为1,即4x2+2
•
x+4 的最小值为1.令
•
=t.g(x)=4x2+2
•
x+4=4(x+
t)2+4-
t2,再利用二次函数的单调性即可得出.
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:∵|
|=|
|=2,函数f(x)=|
+x
|(x∈R)的最小值为1,
∴
2x2+2
•
x+
2 的最小值为1,
即4x2+2
•
x+4 的最小值为1,
令
•
=t.
令g(x)=4x2+2
•
x+4=4(x+
t)2+4-
t2,
当且仅当x=-
t时,g(x)取得最小值4-
t2.
因此4-
t2=1,解得t=±2
.
∴
•
=±2
.
故答案为:±2
.
| a |
| b |
| a |
| b |
∴
| b |
| a |
| b |
| a |
即4x2+2
| a |
| b |
令
| a |
| b |
令g(x)=4x2+2
| a |
| b |
| 1 |
| 4 |
| 1 |
| 4 |
当且仅当x=-
| 1 |
| 4 |
| 1 |
| 4 |
因此4-
| 1 |
| 4 |
| 3 |
∴
| a |
| b |
| 3 |
故答案为:±2
| 3 |
点评:本题考查了向量的数量积运算、二次函数的单调性,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=(
)x2+1(x∈[-1,2])的值域为( )
| 1 |
| 2 |
A、[
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
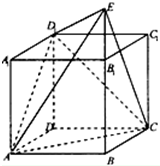 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.