题目内容

设数列{an}满足
a1=2
an=2+
2
an-1
，则a3=
 
．
考点：数列递推式
专题：等差数列与等比数列
分析：利用递推公式求解．
解答： 解：∵数列{an}满足
a1=2
an=2+
2
an-1
，
∴a2=2+
2
2
=3，
a3=2+
2
3
=
8
3
．
故答案为：
8
3
．
点评：本题考查数列的第3项的求法，是基础题，解题时要注意递推思想的合理运用．
练习册系列答案
相关题目
已知Sn是数列{an}的前n项和，若Sn=2n-1，则a1=
 
．
在等差数列{an}中，已知a3=5，a1+a2+…+a7=49
（Ⅰ）求an；
（Ⅱ）若bn=
1
anan+1
（n∈N*），求数列{bn}的前n项和Sn．
已知|
a
|=|
b
|=2，若函数f（x）=|
a
+x
b
|（x∈R）的最小值为1，则
a
•
b
=
 
．
点M（2，1）是抛物线x2=2py上的点，则以点M为切点的抛物线的切线方程为
 
．
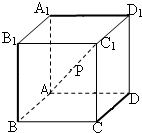在正方体AC1中，若点P在对角线AC1上，且P点到三条棱CD、A1D1、BB1的距离都相等，则这样的点共有（　　）
A、1个B、2个
C、3个D、无穷多个
若函数f（x）=x3-ax2+4在区间[0，2]内单调递减，则（　　）
A、a≥3B、a=3
C、a≤3D、0＜a＜3
若方程x3-x+1=0在区间（a，b）（a，b，∈Z，且b-a=1）上有一根，则a+b的值为（　　）
A、-1B、-2C、-3D、-4
设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1+1，n∈N*，且a1=1．
（1）求数列{an}的通项公式；
（2）求数列{
nan
3n
}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网