题目内容
已知数列{an}中,an+1=
,a1=1,则a2014= .
| an |
| 3an+1 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:取倒数,确定{
}是以1为首项,3为公差的等差数列,确定数列的通项,即可求出a2014.
| 1 |
| an |
解答:
解:∵an+1=
,
∴
-
=3,
∵a1=1,
∴{
}是以1为首项,3为公差的等差数列,
∴
=3n-2,
∴an=
,
∴a2014=
.
故答案为:
.
| an |
| 3an+1 |
∴
| 1 |
| an+1 |
| 1 |
| an |
∵a1=1,
∴{
| 1 |
| an |
∴
| 1 |
| an |
∴an=
| 1 |
| 3n-2 |
∴a2014=
| 1 |
| 6040 |
故答案为:
| 1 |
| 6040 |
点评:本题考查数列递推式,考查数列的通项,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
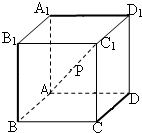 在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
已知l,m,n是三条不同的直线,α,β是两个不同的平面,下列命题为真命题的是( )
| A、若l⊥m,l⊥n,m?α,n?α,则l⊥α |
| B、若l⊥α,α∥β,m?β,则l⊥m |
| C、若l∥m,m?α,则l∥α |
| D、若l⊥α,α⊥β,m?β,则l∥m |
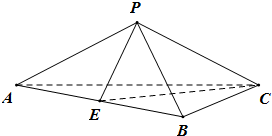 如图,在三棱锥P-ABC中,AB=2
如图,在三棱锥P-ABC中,AB=2