题目内容
设等差数列{an}、等比数列{bn}首项都是1,公差与公比都是2,则ab1+ab2+ab3+ab4+ab5= .
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:由已知条件推导出an=2n-1,bn=2n-1,从而得到ab1+ab2+ab3+ab4+ab5=a1+a2+a4+a8+a16,由此能求出结果.
解答:
解:∵等差数列{an}和等比数列{bn}首项都是1,公差与公比都是2,
∴an=1+(n-1)×2=2n-1,
bn=2n-1,
∴ab1+ab2+ab3+ab4+ab5
=a1+a2+a4+a8+a16
=1+3+7+15+31
=57.
故答案为:57.
∴an=1+(n-1)×2=2n-1,
bn=2n-1,
∴ab1+ab2+ab3+ab4+ab5
=a1+a2+a4+a8+a16
=1+3+7+15+31
=57.
故答案为:57.
点评:本题考查数列的前n项和的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
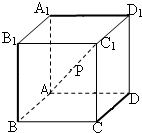 在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )
在正方体AC1中,若点P在对角线AC1上,且P点到三条棱CD、A1D1、BB1的距离都相等,则这样的点共有( )| A、1个 | B、2个 |
| C、3个 | D、无穷多个 |
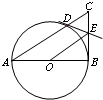 以Rt△ABC的直角边AB为直径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=6,AB=8,则OE=
以Rt△ABC的直角边AB为直径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=6,AB=8,则OE=