题目内容
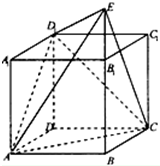 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.(1)求二面角E-AC-D1的余弦值;
(2)在D1E上是否存在一点P,使A1P∥面EAC?若存在,求D1P:PE的值;若不存在,请说明理由.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)设AC∩BD=O,建立空间直角坐标系O-xyz,利用向量法能求出二面角E-AC-D1的余弦值.
(2)设
=λ
=λ(
-
),由A1P∥面EAC,解得λ=
,由此推导出存在点P使A1P∥面EAC,此时D1P:PE=3:2.
(2)设
| D1P |
| PE |
| D1E |
| D1P |
| 3 |
| 2 |
解答:
解:(1)设AC∩BD=O,如图所示建立空间直角坐标系O-xyz,
则A(
,0,0),B(0,1,0),C(-
,0,0),D(0,-1,0),D1(0,-1,2),
设E(0,1,2+h),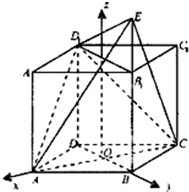
则
=(0,2,h),
=(2
,0,0),
=(
,1,-2),
∵D1E⊥平面D1AC,∴D1E⊥AC,D1E⊥D1A,
∴2-2h=0,解得h=1,即E(0,1,3).
∴
=(0,2,1),
=(-
,1,3).
设平面EAC的法向量为
=(x,y,z),
则由
.
令z=-1,得平面EAC的一个法向量为
=(0,3,-1).
又平面D1AC的法向量为
=(0,2,1),
∴cos<
,
>=
=
,
∴二面角E-AC-D1的余弦值为
.
(2)设
=λ
=λ(
-
),得
=
=(0,
,
),
∴
=
+
=(-
,
,
)
∵A1P∥面EAC,∴
⊥
,
∴-
×0+3×
+(-1)×
=0,解得λ=
,
∴存在点P使A1P∥面EAC,此时D1P:PE=3:2.
则A(
| 3 |
| 3 |
设E(0,1,2+h),

则
| D1E |
| CA |
| 3 |
| D1A |
| 3 |
∵D1E⊥平面D1AC,∴D1E⊥AC,D1E⊥D1A,
∴2-2h=0,解得h=1,即E(0,1,3).
∴
| D1E |
| AE |
| 3 |
设平面EAC的法向量为
| m |
则由
|
令z=-1,得平面EAC的一个法向量为
| m |
又平面D1AC的法向量为
| D1E |
∴cos<
| m |
| D1E |
| 6-1 | ||||
|
| ||
| 2 |
∴二面角E-AC-D1的余弦值为
| ||
| 2 |
(2)设
| D1P |
| PE |
| D1E |
| D1P |
| D1P |
| λ |
| 1+λ |
| D1E |
| 2λ |
| 1+λ |
| λ |
| 1+λ |
∴
| A1P |
| A1D1 |
| D1P |
| 3 |
| λ-1 |
| 1+λ |
| λ |
| 1+λ |
∵A1P∥面EAC,∴
| A1P |
| m |
∴-
| 3 |
| λ-1 |
| 1+λ |
| λ |
| 1+λ |
| 3 |
| 2 |
∴存在点P使A1P∥面EAC,此时D1P:PE=3:2.
点评:本题考查二面角的余弦值的求法,考查满足条件的点的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
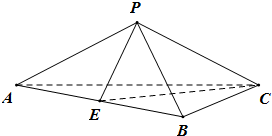 如图,在三棱锥P-ABC中,AB=2
如图,在三棱锥P-ABC中,AB=2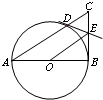 以Rt△ABC的直角边AB为直径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=6,AB=8,则OE=
以Rt△ABC的直角边AB为直径作圆O,圆O与斜边AC交于D,过D作圆O的切线与BC交于E,若BC=6,AB=8,则OE=