题目内容
10.(1)计算化简求值:($\frac{8}{27}$)${\;}^{-\frac{1}{3}}$+log2(2-3×$\frac{1}{64}$)+($\sqrt{2}$-1)ln1+2lg$\sqrt{50}$-lg5+2${\;}^{lo{g}_{2}5}$.(2)已知10a=2,b=lg3,试用a,b表示log630.
分析 (1)利用对数、指数的性质、运算法则求解.
(2)利用对数性质、运算法则、换底公式求解.
解答 解:(1)($\frac{8}{27}$)${\;}^{-\frac{1}{3}}$+log2(2-3×$\frac{1}{64}$)+($\sqrt{2}$-1)ln1+2lg$\sqrt{50}$-lg5+2${\;}^{lo{g}_{2}5}$.
=($\frac{2}{3}$)-2+log22-9+1+$lg\frac{50}{5}$+5
=$\frac{9}{4}-9+1+1+5$
=$\frac{1}{4}$.
(2)∵10a=2,b=lg3,∴a=lg2,
∴log630=$\frac{lg(3×10)}{lg(2×3)}$=$\frac{lg3+1}{lg2+lg3}$=$\frac{b+1}{a+b}$.
点评 本题考查对数式、指数式化简求值,是基础题,注意对数、指数的性质、运算法则的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知tan(α+$\frac{π}{4}$)=$\frac{1}{2}$,且α∈(-$\frac{π}{2}$,0),则$\frac{{2{{sin}^2}α+sin2α}}{{cos(α-\frac{π}{4})}}$=( )
| A. | $-\frac{{3\sqrt{5}}}{10}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
18.已知函数f(x)=cos(ωx+φ)(ω>0)图象的两条相邻对称轴之间距离是$\frac{π}{2}$,若f(x)≤f($-\frac{7π}{8}$),则函数y=sin(ωx+φ)一个单调递增区间是( )
| A. | $[-\frac{3π}{8},\frac{π}{8}]$ | B. | $[\frac{π}{8},\frac{5π}{8}]$ | C. | $[-\frac{5π}{8},-\frac{π}{8}]$ | D. | $[-\frac{π}{8},\frac{3π}{8}]$ |
5.“m>0,n>0”是“方程mx2+ny2=1”表示椭圆的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
20.过点P(1,1)作直线l,与两坐标轴相交所得三角形面积为4,则直线l有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
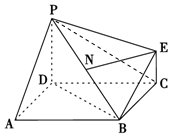 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.