题目内容
20.已知tan(α+$\frac{π}{4}$)=$\frac{1}{2}$,且α∈(-$\frac{π}{2}$,0),则$\frac{{2{{sin}^2}α+sin2α}}{{cos(α-\frac{π}{4})}}$=( )| A. | $-\frac{{3\sqrt{5}}}{10}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
分析 由条件利用两角和的正切公式求得tanα的值,再利用同角三角函数的基本关系,求得$\frac{{2{{sin}^2}α+sin2α}}{{cos(α-\frac{π}{4})}}$的值.
解答 解:∵tan(α+$\frac{π}{4}$)=$\frac{tanα+1}{1-tanα}$=$\frac{1}{2}$,则tanα=-$\frac{1}{3}$,
∵tanα=$\frac{sinα}{cosα}$,sin2α+cos2α=1,α∈(-$\frac{π}{2}$,0),
可得 sinα=-$\frac{\sqrt{10}}{10}$.
∴$\frac{{2{{sin}^2}α+sin2α}}{{cos(α-\frac{π}{4})}}$=$\frac{2sinα(sinα+cosα)}{cos(\frac{π}{4}-α)}$=$\frac{4sinα(sinα+cosα)}{\sqrt{2}(sinα+cosα)}$=2$\sqrt{2}$sinα=2$\sqrt{2}$×(-$\frac{\sqrt{10}}{10}$)=-$\frac{2\sqrt{5}}{5}$.
故选:B.
点评 本题主要考查两角和的正切公式的应用,同角三角函数的基本关系,属于基础题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
10.某三棱锥的三视图如图所示,则该三棱锥的表面积为( )
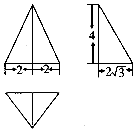
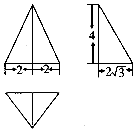
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
15.已知全集U={x|x≤5},集合A={x|-3<x<4},B={x|-5≤x≤3},则(∁UA)∩B=( )
| A. | {x|-5≤x≤-3} | B. | {x|4<x<5,或x≤-3} | C. | {x|-5<x<-3} | D. | {x|-5<x<5} |
12.已知函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$,则函数f(x)的值域是( )
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
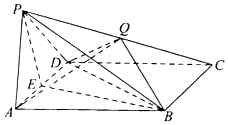 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.