题目内容
1.已知函数f(x)=|x+1|-|x-1|+a(a∈R).(Ⅰ)若a=1,求不等式f(x)≥0的解集;
(Ⅱ)若方程f(x)=x有三个实数根,求实数a的取值范围.
分析 (Ⅰ)根据绝对值的意义,求得不等式f(x)≤6的解集.
(Ⅱ)函数f(x)的图象与直线y=x有3个不同的交点,数形结合可得a的范围.
解答 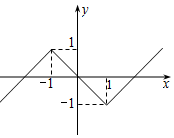 解:(Ⅰ)∵a=1时,f(x)=|x+1|-|x-1|+1,
解:(Ⅰ)∵a=1时,f(x)=|x+1|-|x-1|+1,
∴当x≤-1时,f(x)=-1,不可能非负.
当-1<x<1时,f(x)=2x+1,由f(x)≥0可解得x≥$-\frac{1}{2}$,于是$-\frac{1}{2}$≤x<1.
当x≥1时,f(x)=3>0恒成立.
∴不等式f(x)≥0的解集$[-\frac{1}{2}\;,\;\;+∞)$.…(5分)
(Ⅱ)由方程f(x)=x可变形为a=x+|x-1|-|x+1|.
令$h(x)=x+|{x-1}|-|{x+1}|=\left\{\begin{array}{l}x+2,x<-1\\-x,\;\;\;-1≤x≤1\\ x-2,x>1\end{array}\right.$
作出图象如右. …(8分)
于是由题意可得-1<a<1.…(10分)
点评 本题主要绝对值的意义,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
12.已知函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$,则函数f(x)的值域是( )
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
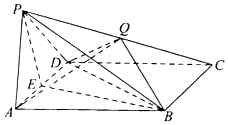 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.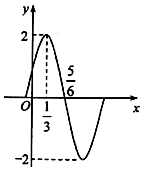 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的图象(部分)如图.
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|<\frac{π}{2}})$的图象(部分)如图.