题目内容
16.在直角坐标系xOy中,曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=1+tsinα}\end{array}\right.$(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2=4$\sqrt{2}$ρsin(θ+$\frac{π}{4}$)-4.(Ⅰ)求曲线C2的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)若曲线C1与曲线C2交于A、B两点,求|AB|的最大值和最小值.
分析 (Ⅰ)∵曲线C2的极坐标方程转化为ρ2=4ρsinθ+4ρcosθ-4,由ρ2=x2+y2,ρsinθ=y,ρcosθ=x,得:(x-2)2+(y-2)2=4,由此得到曲线C2表示以(2,2)为圆心,以2为半径的圆.
(Ⅱ)消去参数得曲线C1的直角坐标方程为tanα•x-y-tanα+1=0,求出圆心C2(2,2)到曲线C1:tanα•x-y-tanα+1=0的距离d,|AB|=2×$\sqrt{{r}^{2}-{d}^{2}}$,由此能求出结果.
解答 解:(Ⅰ)∵曲线C2的极坐标方程为ρ2=4$\sqrt{2}$ρsin(θ+$\frac{π}{4}$)-4=4ρsinθ+4ρcosθ-4,
∴由ρ2=x2+y2,ρsinθ=y,ρcosθ=x,
得到曲线C2的直角坐标方程为:x2+y2=4y+4x-4,
整理,得:(x-2)2+(y-2)2=4,
∴曲线C2表示以(2,2)为圆心,以2为半径的圆.
(Ⅱ)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=1+tsinα}\end{array}\right.$(t为参数),
∴消去参数得曲线C1的直角坐标方程为tanα•x-y-tanα+1=0,
当曲线C1过圆心C2(2,2)时,tanα=1,α=45°,
此时|AB|取最大值2r=2$\sqrt{2}$.
圆心C2(2,2)到曲线C1:tanα•x-y-tanα+1=0的距离为:
d=$\frac{|2tanα-2-tanα+1|}{\sqrt{ta{n}^{2}α+1}}$=$\frac{|tanα-1|}{\sqrt{ta{n}^{2}α+1}}$,
|AB|=2×$\sqrt{{r}^{2}-{d}^{2}}$=2$\sqrt{2-\frac{ta{n}^{2}α+1-2tanα}{ta{n}^{2}α+1}}$=2$\sqrt{1+\frac{2tanα}{ta{n}^{2}α+1}}$,
∴当tanα=0,即α=0时,|AB|取最小值2.
点评 本小题主要考查曲线的直角坐标方程的求法,考查弦长的最值的求法,考查参数方程、极坐标等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,是中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案| A. | 16π | B. | 64π | C. | $\frac{32}{3}$π | D. | 32π |
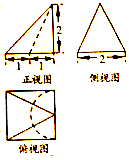 某零件的三视图如图所示,则该零件的体积为( )
某零件的三视图如图所示,则该零件的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
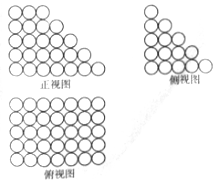 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积,设隙积共n层,上底由a×b个物体组成,以下各层的长、宽依次各增加一个物体,最下层(即下底)由c×d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}$[(2b+d)a+(b+2d)c]+$\frac{n}{6}$(c-a).已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为( )
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积,设隙积共n层,上底由a×b个物体组成,以下各层的长、宽依次各增加一个物体,最下层(即下底)由c×d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}$[(2b+d)a+(b+2d)c]+$\frac{n}{6}$(c-a).已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为( )