题目内容
6．在长方体ABCD-A1B1C1D1中，底面ABCD是边长为$\sqrt{2}$的正方形，AA1=3，E是AA1的中点，过C1作C1F⊥平面BDE与平面ABB1A1交于点F，则$\frac{AF}{A{A}_{1}}$=$\frac{5}{9}$．分析 连结AC、BD，交于点O，当C1F与EO垂直时，C1F⊥平面BDE，
从而F∈AA1，△C1A1F∽△EAO，由此能求出$\frac{AF}{{AA}_{1}}$的值．
解答 解：连结AC、BD，交于点O，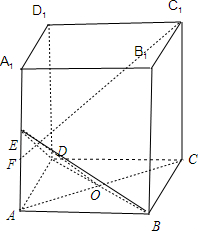
∵四边形ABCD是正方形，AA1⊥底面ABCD，
∴BD⊥平面ACC1A1，
则当C1F与EO垂直时，C1F⊥平面BDE，
∵F∈平面ABB1A1，∴F∈AA1，
在矩形ACC1A1中，△C1A1F∽△EAO，
则$\frac{{{A}_{1}C}_{1}}{{A}_{1}F}$=$\frac{AE}{AO}$，
∵A1C1=2AO=$\sqrt{2}$AB=2，AE=$\frac{3}{2}$，AA1=3，
∴A1F=$\frac{4}{3}$，∴AF=$\frac{5}{3}$，∴$\frac{AF}{{AA}_{1}}$=$\frac{5}{9}$．
故答案为：$\frac{5}{9}$
点评 本题考查两线段的比值的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同，F1，F2为椭圆的左、右焦点．M为椭圆上任意一点，△MF1F2面积的最大值为4$\sqrt{2}$．
15．命题“对任意的x∈R，x3-x+1≤0”的否定是（ ）
| A． | 不存在x∈R，x3-x+1≤0 | B． | 存在x∈R，x3-x+1≤0 | ||
| C． | 对任意的x∈R，x3-x+1＞0 | D． | 存在x∈R，x3-x+1＞0 |