题目内容

4．已知M是函数f（x）=e-2|x-1|+2sin[π（x-$\frac{1}{2}$）]在x∈[-3，5]上的所有零点之和，则M的值为（　　）
A．4B．6C．8D．10

分析 函数的零点，转化为两个函数的图形的交点的横坐标，利用函数的对称性，求解即可．

解答 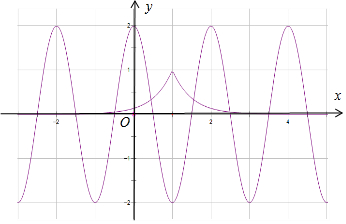解：函数f（x）=e-2|x-1|+2sin[π（x-$\frac{1}{2}$）]在x∈[-3，5]上的所有零点，就是e-2|x-1|=-2sin[π（x-$\frac{1}{2}$）]在x∈[-3，5]上的所有的根，即e-2|x-1|=2cosπx在x∈[-3，5]上的所有根，就是函数y=e-2|x-1|与y=2cosπx，交点的横坐标，画出两个函数的图象如图，因为两个函数都关于x=1对称，两个函数共有8个交点，所以函数f（x）=e-2|x-1|+2sin[π（x-$\frac{1}{2}$）]在x∈[-3，5]上的所有零点之和，M=8．
故选：C．

点评 本题考查函数的零点与方程根的关系，考查数形结合以及转化思想的应用，考查计算能力．

练习册系列答案
相关题目
14．已知椭圆Γ：$\frac{x^2}{a^2}$+y2=1（a＞1）的左焦点为F1，右顶点为A1，上顶点为B1，过F1，A1，B1三点的圆P的圆心坐标为（$\frac{{\sqrt{3}-\sqrt{2}}}{2}$，$\frac{{1-\sqrt{6}}}{2}$）．
（Ⅰ）求椭圆的方程；
（Ⅱ）若直线l：y=kx+m（k，m为常数，k≠0）与椭圆Γ交于不同的两点M和N．
（i）当直线l过E（1，0），且$\overrightarrow{EM}$+2$\overrightarrow{EN}$=$\overrightarrow 0$时，求直线l的方程；
（ii）当坐标原点O到直线l的距离为$\frac{{\sqrt{3}}}{2}$时，求△MON面积的最大值．
15．命题“对任意的x∈R，x3-x+1≤0”的否定是（　　）
A．不存在x∈R，x3-x+1≤0B．存在x∈R，x3-x+1≤0
C．对任意的x∈R，x3-x+1＞0D．存在x∈R，x3-x+1＞0
12．若（x+y）3（2x-y+a）5的展开式中各项系数的和为256，则该展开式中含字母x且x的次数为1的项的系数为0．
19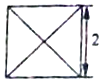．已知某几何体的俯视图是如图所示的边长为2的正方形，主视图与左视图是边长为2的正三角形，则其侧面积（　　）
A．4B．$4\sqrt{3}$C．$4（1+\sqrt{3}）$D．8
9．若函数f（x）=$\left\{\begin{array}{l}{\frac{1}{{2}^{x}}-1，x＜1}\\{\frac{lnx}{{x}^{2}}，x≥1}\end{array}\right.$，则函数y=|f（x）|-$\frac{1}{8}$的零点个数为4．
16．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+tcosα}\\{y=1+tsinα}\end{array}\right.$（t为参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2=4$\sqrt{2}$ρsin（θ+$\frac{π}{4}$）-4．
（Ⅰ）求曲线C2的直角坐标方程，并指出其表示何种曲线；
（Ⅱ）若曲线C1与曲线C2交于A、B两点，求|AB|的最大值和最小值．
13．已知四棱锥P-ABCD的顶点都在球O的球面上，底面ABCD是矩形，平面PAD⊥底面ABCD，△PAD为正三角形，AB=2AD=4，则球O的表面积为（　　）
A．$\frac{56π}{3}$B．$\frac{64π}{3}$C．24πD．$\frac{80π}{3}$
14．执行如图所示的程序框图，若输入n=10，则输出S=（　　）
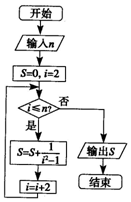
A．$\frac{4}{9}$B．$\frac{5}{11}$C．$\frac{6}{13}$D．$\frac{36}{55}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网