题目内容
5.已知O是坐标原点,A,B分别是函数y=sinπx以O为起点的一个周期内的最大值点和最小值点.则tan∠OAB=$\frac{4}{3}$.分析 根据题意画出图形,结合图形,利用函数y=sinπx的对称性得出∠OAB=2∠OAC,结合二倍角公式求出tan∠OAB的值.
解答 解:如图所示;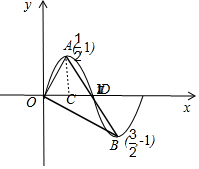
O是坐标原点,A,B分别是函数y=sinπx以O为起点的一个周期内的最大值点和最小值点,
∴AB过点D,且∠OAB=2∠OAC;
又A($\frac{1}{2}$,1),
∴tan∠OAC=$\frac{1}{2}$,
∴tan∠OAB=$\frac{2tan∠OAC}{1{-tan}^{2}∠OAC}$=$\frac{2×\frac{1}{2}}{1{-(\frac{1}{2})}^{2}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题主要考查了三角函数的图象与性质的应用问题,也考查了直角三角形中边角关系的应用问题,是基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
15.命题“对任意的x∈R,x3-x+1≤0”的否定是( )
| A. | 不存在x∈R,x3-x+1≤0 | B. | 存在x∈R,x3-x+1≤0 | ||
| C. | 对任意的x∈R,x3-x+1>0 | D. | 存在x∈R,x3-x+1>0 |
13.已知四棱锥P-ABCD的顶点都在球O的球面上,底面ABCD是矩形,平面PAD⊥底面ABCD,△PAD为正三角形,AB=2AD=4,则球O的表面积为( )
| A. | $\frac{56π}{3}$ | B. | $\frac{64π}{3}$ | C. | 24π | D. | $\frac{80π}{3}$ |
20.已知等差数列{an}满足:a2=2,Sn-Sn-3=54(n>3),Sn=100,则n=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
10.设$f(x)=\left\{\begin{array}{l}x+4,x≤-2或x≥3\\{x^2}-1,-2<x<3\end{array}\right.$,若函数y=f(x)+k的图象与x轴恰有三个不同交点,则k的取值范围是( )
| A. | (-2,1) | B. | [0,1] | C. | [-2,0) | D. | [-2,1) |
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )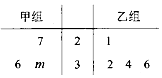

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
14.执行如图所示的程序框图,若输入n=10,则输出S=( )
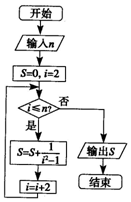

| A. | $\frac{4}{9}$ | B. | $\frac{5}{11}$ | C. | $\frac{6}{13}$ | D. | $\frac{36}{55}$ |