题目内容
7.$\underset{lim}{n→∞}\frac{(2n-3)^{2}}{3{n}^{2}-n+7}$=$\frac{4}{3}$.分析 利用洛必达法则对所求分式变形求极限值.
解答 解:原式=$\underset{lim}{n→∞}\frac{4{n}^{2}-12n+9}{3{n}^{2}-n+7}$=$\underset{lim}{n→∞}\frac{4-\frac{12}{n}+\frac{9}{{n}^{2}}}{3-\frac{1}{n}+\frac{7}{{n}^{2}}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$
点评 本题考查了利用洛必达法则求$\frac{∞}{∞}$型的分式的极限;属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
15.命题“对任意的x∈R,x3-x+1≤0”的否定是( )
| A. | 不存在x∈R,x3-x+1≤0 | B. | 存在x∈R,x3-x+1≤0 | ||
| C. | 对任意的x∈R,x3-x+1>0 | D. | 存在x∈R,x3-x+1>0 |
2. 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,点M∈AB1,N∈BC1,且AM=BN≠$\sqrt{2}$,有以下四个结论:①AA1⊥MN;②AB∥MN;③MN∥平面A1B1C1D1;④MN与A1C1一定是异面直线.其中正确命题的序号是( )| A. | ①③ | B. | ②③ | C. | ①④ | D. | ①③④ |
19.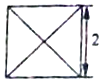 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
 已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )
已知某几何体的俯视图是如图所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其侧面积( )| A. | 4 | B. | $4\sqrt{3}$ | C. | $4(1+\sqrt{3})$ | D. | 8 |
17.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为( )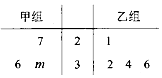

| A. | 32 | B. | 33 | C. | 34 | D. | 35 |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同,F1,F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4$\sqrt{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点与抛物线${y^2}=8\sqrt{2}x$的焦点相同,F1,F2为椭圆的左、右焦点.M为椭圆上任意一点,△MF1F2面积的最大值为4$\sqrt{2}$.