题目内容
 如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=
如图,底面是等腰梯形的四棱锥E-ABCD中,EA⊥平面ABCD,AB∥CD,AB=2CD,∠ABC=| π |
| 3 |
(Ⅰ)设F为EA的中点,证明:DF∥平面EBC;
(Ⅱ)若AE=AB=2,求三棱锥B-CDE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)取EB的中点G,连接FG,CG,利用F为EA的中点,证明四边形CDFG为平行四边形,即可证明:DF∥平面EBC;
(Ⅱ)等腰梯形ABCD中,作CH⊥AB于H,求出点B到CD的距离,即可求三棱锥B-CDE的体积.
(Ⅱ)等腰梯形ABCD中,作CH⊥AB于H,求出点B到CD的距离,即可求三棱锥B-CDE的体积.
解答:
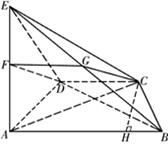 (Ⅰ)证明:取EB的中点G,连接FG,CG,
(Ⅰ)证明:取EB的中点G,连接FG,CG,
∵F为EA的中点,
∴FG∥AB,FG=
AB,
∵AB∥CD,AB=2CD,
∴FG∥CD,FG=CD,
∴四边形CDFG为平行四边形,
∴DF∥CG,
∵DF?平面EBC,CG?平面EBC,
∴DF∥平面EBC;
(Ⅱ)解:等腰梯形ABCD中,作CH⊥AB于H,则BH=
,
在Rt△BHC中,∠ABC=60°,则CH=
tan60°=
,
即点C到AB的距离d=
,则点B到CD的距离为
,
∵EA⊥平面ACD,
∴三棱锥B-CDE的体积为VE-BDC=
•
•1•
•2=
.
 (Ⅰ)证明:取EB的中点G,连接FG,CG,
(Ⅰ)证明:取EB的中点G,连接FG,CG,∵F为EA的中点,
∴FG∥AB,FG=
| 1 |
| 2 |
∵AB∥CD,AB=2CD,
∴FG∥CD,FG=CD,
∴四边形CDFG为平行四边形,
∴DF∥CG,
∵DF?平面EBC,CG?平面EBC,
∴DF∥平面EBC;
(Ⅱ)解:等腰梯形ABCD中,作CH⊥AB于H,则BH=
| 1 |
| 2 |
在Rt△BHC中,∠ABC=60°,则CH=
| 1 |
| 2 |
| ||
| 2 |
即点C到AB的距离d=
| ||
| 2 |
| ||
| 2 |
∵EA⊥平面ACD,
∴三棱锥B-CDE的体积为VE-BDC=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 6 |
点评:本题考查线面平行,考查三棱锥的体积,考查学生分析解决问题的能力,难度中等.

练习册系列答案
相关题目
已知奇函数f(x)在x≥0时,f(x)=x2-4x,则使f(x-2)>-3成立的x的取值范围是( )
A、(-2-
| ||
B、(-4-
| ||
C、(-
| ||
D、(-∞,-
|
若实数a,b,c,d满足a>b,c>d,则下列不等式成立的是( )
| A、a-c>b-d | ||||
| B、a+c>b+d | ||||
| C、ac>bd | ||||
D、
|
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点. 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N. 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=