题目内容
求函数y=
的最小正周期．
sin2x+sin(2x+
| ||
cos2x+cos(2x+
|
考点：两角和与差的正弦函数,三角函数的周期性及其求法
专题：三角函数的求值
分析：利用两角和的正弦与余弦可化简y=
=tan（2x+
），从而可求得其最小正周期．
sin2x+sin(2x+
| ||
cos2x+cos(2x+
|
| π |
| 6 |
解答：
解：原式=
=
=tan（2x+
），
其最小正周期T=
．
故函数y=
的最小正周期为π．
sin2x+
| ||||||
cos2x+
|
| ||||
|
| π |
| 6 |
其最小正周期T=
| π |
| 2 |
故函数y=
sin2x+sin(2x+
| ||
cos2x+cos(2x+
|
点评：本题考查两角和的正弦与余弦，考查辅助角公式的应用，突出考查三角函数的周期性及其求法，属于中档题．
练习册系列答案
相关题目
已知α∈（0，
），sinα=
，则cos（
-α）等于（ ）
| π |
| 2 |
| 4 |
| 5 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若函数f（x）=logax的图象与直线y=
x相切，则a的值为（ ）
| 1 |
| 3 |
A、e
| ||
B、e
| ||
C、
| ||
D、e
|
设等比数列{an}满足a1+a2=1，a3+a4=3，则a5+a6=（ ）
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
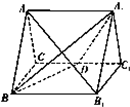如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
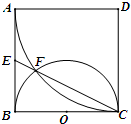如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．
如图，底面是等腰梯形的四棱锥E-ABCD中，EA⊥平面ABCD，AB∥CD，AB=2CD，∠ABC=