题目内容
已知点A（a，0），B（0，b）（其中a，b均大于4），直线AB与圆C：x2+y2-4x-4y+4=0 相切．
（1）求证：（a-4）（b-4）=8
（2）求线段AB的中点M的轨迹方程．
（1）求证：（a-4）（b-4）=8
（2）求线段AB的中点M的轨迹方程．
考点：直线与圆的位置关系
专题：直线与圆
分析：（1）由条件利用直线和圆相切的性质可得圆心到切线的距离等于半径，化简可得结论．
（2）设线段AB的中点M的坐标为（x，y），则a=2x，b=2y，再根据（a-4）（b-4）=8化简可得结论．
（2）设线段AB的中点M的坐标为（x，y），则a=2x，b=2y，再根据（a-4）（b-4）=8化简可得结论．
解答：
（1）证明：∵直线AB的方程为
+
=1，即bx+ay-ab=0，
因为直线AB与圆C：（x-2）2+（y-2）2=4相切，所以
=2．
所以ab-4b-4a+8=0，即（a-4）（b-4）=8．
（2）设线段AB的中点M的坐标为（x，y），则a=2x，b=2y，
所以（2x-4）（2y-4）=8，即（x-2）（y-2）=2，（x＞2，y＞2）．
即线段AB的中点M的轨迹方程为（x-2）（y-2）=2，（x＞2，y＞2）．
| x |
| a |
| y |
| b |
因为直线AB与圆C：（x-2）2+（y-2）2=4相切，所以
| |2b+2a-ab| | ||
|
所以ab-4b-4a+8=0，即（a-4）（b-4）=8．
（2）设线段AB的中点M的坐标为（x，y），则a=2x，b=2y，
所以（2x-4）（2y-4）=8，即（x-2）（y-2）=2，（x＞2，y＞2）．
即线段AB的中点M的轨迹方程为（x-2）（y-2）=2，（x＞2，y＞2）．
点评：本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，线段的中点公式，求点的轨迹方程，属于基础题．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
集合A={x|x2-2x＜0}，B={y|y=2x，x＞0}，R是实数集，则A∩B=（ ）
| A、（0，+∞） |
| B、（-∞，0）∪（2，+∞） |
| C、（0，1） |
| D、（1，2） |
设等比数列{an}满足a1+a2=1，a3+a4=3，则a5+a6=（ ）
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
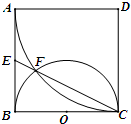如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．
如图，底面是等腰梯形的四棱锥E-ABCD中，EA⊥平面ABCD，AB∥CD，AB=2CD，∠ABC=
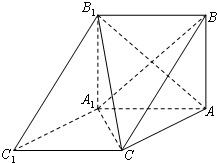如图，三棱柱ABC-A1B1C1中，BA⊥平面AA1C1C，AB=2
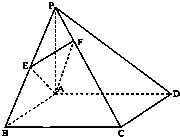如图，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AB，