题目内容
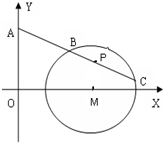如图，过点A（0，a）作直线l，交圆M：（x-2）2+y2=1于点B、C，在BC上取一点P，使P点满足| AB |
| AC |
| BP |
| PC |
（1）求动点P的轨迹方程；
（2）若点P的轨迹交圆M于点R、S，求△MRS面积的最大值．
考点：轨迹方程
专题：综合题,向量与圆锥曲线
分析：（1）分别设出P、A、B、C的坐标，求出向量的坐标，由向量共线的条件得到坐标关系，联立直线与圆的方程，化为关于x的一元二次方程后利用根与系数关系得到B，C的横坐标的和与积，表示出P点坐标，消去参数k求得P的轨迹；
（2）联立P的轨迹方程和圆的方程，把△MRS面积转化为两个三角形面积的和，换元后利用函数的单调性求最值．
（2）联立P的轨迹方程和圆的方程，把△MRS面积转化为两个三角形面积的和，换元后利用函数的单调性求最值．
解答：
解：（1）设P（x，y），A（xA，yA），B（xB，yB），C（xC，yC），
∵
=λ
，
=λ
（λ∈R），
∴xB=λxC，x-xB=λ（xC-x），
∴
=
，
∴x=
①
设过点A（0，a）的直线l的方程为y=kx+a，
联立
，得（1+k2）x2+（2ak-4）x+a2+3=0．
则xB+xC=
，xBxC=
．
代入①得：x=
，y=kx+a=
．
消去k，得2x-ay-3=0（在圆M内的部分）；
（2）设R（x3，y3），S（x4，y4），
联立
，得（a2+4）y2-2ay-3=0．
y3+y4=
，y3y4=
．
则|y3-y4|=
=4
．
∴S△MRS=
×
×4
=
=
．
令t=a2+3（t≥3），而函数f（t）=t+
在[3，+∞）上为增函数，
∴S△MRS≤
=
．
此时t=3，a=0．
∵
| AB |
| AC |
| BP |
| PC |
∴xB=λxC，x-xB=λ（xC-x），
∴
| x-xB |
| xC-x |
| xB |
| xC |
∴x=
| 2xBxC |
| xB+xC |
设过点A（0，a）的直线l的方程为y=kx+a，
联立
|
则xB+xC=
| 4-2ak |
| 1+k2 |
| a2+3 |
| 1+k2 |
代入①得：x=
| a2+3 |
| 2-ak |
| 2a+3k |
| 2-ak |
消去k，得2x-ay-3=0（在圆M内的部分）；
（2）设R（x3，y3），S（x4，y4），
联立
|
y3+y4=
| 2a |
| a2+4 |
| -3 |
| a2+4 |
则|y3-y4|=
| (y3+y4)2-4y3y4 |
|
∴S△MRS=
| 1 |
| 2 |
| 1 |
| 2 |
|
|
|
令t=a2+3（t≥3），而函数f（t）=t+
| 1 |
| t |
∴S△MRS≤
|
| ||
| 4 |
此时t=3，a=0．
点评：本题考查了轨迹方程，训练了平面向量在解题中的应用，考查了直线与圆的位置关系，体现了数学转化思想方法，训练了利用函数单调性求函数最值，综合考查了学生分析问题和解决问题的能力，考查了计算能力，是高考试卷中的压轴题．
练习册系列答案
相关题目
从231个编号中抽取22个号码入样，若采用系统抽样方法进行抽取，则分段间隔应为（ ）
A、10
| ||
| B、22 | ||
| C、10 | ||
| D、11 |
在△ABC中，角A、B、C的对应边分别为x、b、c，若满足b=2，B=45°的△ABC恰有两解，则x的取值范围是（ ）
| A、（2，+∞） | ||
| B、（0，2） | ||
C、(2，2
| ||
D、(
|