题目内容
已知数列{an}的各项均为正数,Sn为其前n项和,对于任意n∈N*,满足关系Sn=2an-2.
(1)证明:{an}是等比数列;
(2)在正数数列{cn}中,设(cn)n+1=
an+1(n∈N*),求数列{lncn} 中的最大项.
(1)证明:{an}是等比数列;
(2)在正数数列{cn}中,设(cn)n+1=
| (n+1) |
| 2n+1 |
考点:等比关系的确定,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)根据等比数列的定义以及an与Sn的关系即可证明数列{an} 是等比数列,
(2)求出数列{cn}的通项公式以及数列{lncn}的公式,利用导数研究数列数列{lncn}的单调性即可得到结论.
(2)求出数列{cn}的通项公式以及数列{lncn}的公式,利用导数研究数列数列{lncn}的单调性即可得到结论.
解答:
解:(1)∵Sn=2an-2. ①
∴Sn+1=2an+1-2. ②
②-①,得an+1=2an+1-2an.
∵an>0
∴
=2
故数列{an} 是等比数列
∴s1=2a1-2
∴a1=2
∴an=2n
(2)(cn)n+1=
an+1=
•2n+1=n+1
∴cn=
,lncn=
.
则c1c3>c4>???猜想当n≥2时,{cn}是递减函数,
令f(x)=
,则f'(x)=
,
当x≥3时,lnx>1,此时f'(x)<0,
∴当x≥3时,函数f(x)单调递减.
即当n≥2时,{lncn}是递减数列,
又c1<c2,
∴数列{lncn} 中的最大项为c2=
.
∴Sn+1=2an+1-2. ②
②-①,得an+1=2an+1-2an.
∵an>0
∴
| an+1 |
| an |
故数列{an} 是等比数列
∴s1=2a1-2
∴a1=2
∴an=2n
(2)(cn)n+1=
| (n+1) |
| 2n+1 |
| n+1 |
| 2n+1 |
∴cn=
| n+1 | n+1 |
| ln(n+1) |
| n+1 |
则c1c3>c4>???猜想当n≥2时,{cn}是递减函数,
令f(x)=
| lnx |
| x |
| 1-lnx |
| x2 |
当x≥3时,lnx>1,此时f'(x)<0,
∴当x≥3时,函数f(x)单调递减.
即当n≥2时,{lncn}是递减数列,
又c1<c2,
∴数列{lncn} 中的最大项为c2=
| 3 | 3 |
点评:本题主要考查等比数列的定义和应用,以及利用导数研究函数的单调性,综合性较强,难度较大,考查学生的计算能力.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知等差数列{an}满足a2+a12+2a5=120,则a6为( )
| A、40 | B、36 | C、30 | D、15 |
已知x<y<0,则有( )
| A、0<x2<xy |
| B、y2<xy<x2 |
| C、xy<y2<x2 |
| D、y2>x2>0 |
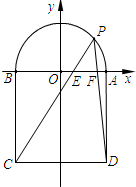 如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.
如图,点P是半圆C:x2+y2=1(y≥0)上位于x轴上方的任意一点,A、B是直径的两个端点,以AB为一边作正方形ABCD,PC交AB于E,PD交AB于F,求证:BE,EF,FA成等比数列.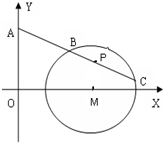 如图,过点A(0,a)作直线l,交圆M:(x-2)2+y2=1于点B、C,在BC上取一点P,使P点满足
如图,过点A(0,a)作直线l,交圆M:(x-2)2+y2=1于点B、C,在BC上取一点P,使P点满足