题目内容
在△ABC中，角A、B、C的对应边分别为x、b、c，若满足b=2，B=45°的△ABC恰有两解，则x的取值范围是（ ）
| A、（2，+∞） | ||
| B、（0，2） | ||
C、(2，2
| ||
D、(
|
考点：正弦定理
专题：解三角形
分析：根据三角形有解的条件建立条件关系即可．
解答：
解：由三角形有两角的充要条件可知xsin45°＜b＜x，
即
x＜2＜x，
解得2＜x＜2
，
即x的取值范围是（2，2
）．
故选：C．
解：由三角形有两角的充要条件可知xsin45°＜b＜x，即
| ||
| 2 |
解得2＜x＜2
| 2 |
即x的取值范围是（2，2
| 2 |
故选：C．
点评：本题主要考查三角形个数的应用，要求熟练掌握三角形有解的等价条件，比较基础．
练习册系列答案
相关题目
若p∧q真命题，则：
①p或q是真命题，
②p且￢q是真命题，
③￢p且￢q是假命题，
④￢p或￢q是假命题，其中正确的是（ ）
①p或q是真命题，
②p且￢q是真命题，
③￢p且￢q是假命题，
④￢p或￢q是假命题，其中正确的是（ ）
| A、①② | B、③④ | C、②④ | D、①③④ |
“?x∈R，x2+x+1＞0“的否定是（ ）
| A、?x0∈R，x02+x0+1＞0 |
| B、?x0∈R，x02+x0+1≤0 |
| C、?x∈R，x2+x+1＞0 |
| D、?x∈R，x2+x+1≤0 |
cos(
-a)等于（ ）
| 3π |
| 2 |
| A、sina | B、cosa |
| C、-sina | D、-cosa |
已知角α的终边过点P（-3，-4），则tanα等于（ ）
| A、-3 | ||
| B、-4 | ||
C、
| ||
D、
|
已知x＜y＜0，则有（ ）
| A、0＜x2＜xy |
| B、y2＜xy＜x2 |
| C、xy＜y2＜x2 |
| D、y2＞x2＞0 |
设全集A={x|x2-2x-15＜0}，B={x|y=lg（x+2）}，则A∩B表示的集合是（ ）
| A、[2，3] |
| B、（-2，5） |
| C、[0，2] |
| D、（2，+∞） |
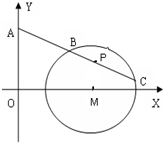如图，过点A（0，a）作直线l，交圆M：（x-2）2+y2=1于点B、C，在BC上取一点P，使P点满足