题目内容
在Z轴上求一点M，使点M到点A（1，0，2）与点B（1，-3，1）的距离相等．
考点：空间两点间的距离公式
专题：计算题,空间位置关系与距离
分析：设出M的坐标，利用空间两点间距离公式，求解即可．
解答：
解：设M（0，0，z），
∵Z轴上一点M到点A（1，0，2）与B（1，-3，1）的距离相等，
∴
=
，
解得z=-3，
∴M的坐标为（0，0，-3）．
故答案为：（0，0，-3）．
∵Z轴上一点M到点A（1，0，2）与B（1，-3，1）的距离相等，
∴
| 12+0+(2-z)2 |
| 12+(0+3)2+(z-1)2 |
解得z=-3，
∴M的坐标为（0，0，-3）．
故答案为：（0，0，-3）．
点评：本题考查空间两点间距离公式的应用，考查计算能力．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
过点A（2，1）的直线与双曲线2x2-y2=2交于P、Q两点，则线段PQ的中点M的轨迹方程是（ ）
| A、2x2-y2-4x+y=0 |
| B、2x2-y2+4x+y=0 |
| C、2x2-y2+4x-y=0 |
| D、2x2-y2-4x-y=0 |
已知角α的终边过点P（-3，-4），则tanα等于（ ）
| A、-3 | ||
| B、-4 | ||
C、
| ||
D、
|
设全集A={x|x2-2x-15＜0}，B={x|y=lg（x+2）}，则A∩B表示的集合是（ ）
| A、[2，3] |
| B、（-2，5） |
| C、[0，2] |
| D、（2，+∞） |
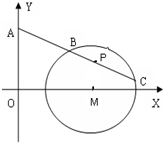如图，过点A（0，a）作直线l，交圆M：（x-2）2+y2=1于点B、C，在BC上取一点P，使P点满足