题目内容
f(x)=
，先分别求f（0）+f（1），f（-1）+f（2），f（-2）+f（3），然后归纳猜想一般性结论，并给出证明．
| 1 | ||
3x+
|
考点：进行简单的合情推理
专题：证明题,函数的性质及应用
分析：由f（x）计算各和式，得出结论然后归纳猜想，再证明一般性结论．
解答：
解：∵f(x)=
，
∴f（0）+f（1）=
+
=
+
=
，
同理可得：f（-1）+f（2）=
，f（-2）+f（3）=
．
猜想f(x)+f(1-x)=
．
证明：设x1+x2=1，
则f（x1）+f（x2）=
+
=
=
．
| 1 | ||
3x+
|
∴f（0）+f（1）=
| 1 | ||
1+
|
| 1 | ||
3+
|
| ||
| 2 |
3-
| ||
| 6 |
| ||
| 3 |
同理可得：f（-1）+f（2）=
| ||
| 3 |
| ||
| 3 |
猜想f(x)+f(1-x)=
| ||
| 3 |
证明：设x1+x2=1，
则f（x1）+f（x2）=
| 1 | ||
3x1+
|
| 1 | ||
3x2+
|
3x1+3x2+2
| ||
|
| ||
| 3 |
点评：本题主要考查归纳推理，一般思路是从具体到一般，得到一般性结论，然后再证明．属中档题．
练习册系列答案
相关题目
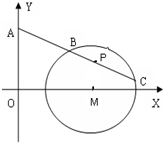如图，过点A（0，a）作直线l，交圆M：（x-2）2+y2=1于点B、C，在BC上取一点P，使P点满足